题目内容
已知双曲线x2-y2=1与直线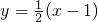
交于A、B两点，满足条件
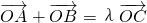（O为坐标原点）的点C也在双曲线上，则点C的个数为
- A.0个
- B.1个
- C.2个
- D.0个或1个或2个
A
分析：联立方程，
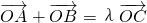可求A，B，设C（x，y）由可求C，再由 点C也在双曲线上，x2-y2=1上代入可求λ的值
解答：联立方程，整理可得3x2+2x-5=0
∴
或
可令A（1，0），B（
），设C（x，y）
∵∴
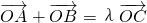∵点C也在双曲线上，x2-y2=1
即
解λ不存在
故选A．
点评：本题主要考查了直线域双曲线的相交求交点，一般是联立方程求解方程的解，向量的基本运算也是解决本题的关键所在．
分析：联立方程，
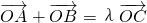可求A，B，设C（x，y）由可求C，再由 点C也在双曲线上，x2-y2=1上代入可求λ的值解答：联立方程，
整理可得3x2+2x-5=0∴
或可令A（1，0），B（），设C（x，y）∵
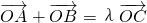∴∵点C也在双曲线上，x2-y2=1
即
解λ不存在故选A．
点评：本题主要考查了直线域双曲线的相交求交点，一般是联立方程求解方程的解，向量的基本运算也是解决本题的关键所在．
练习册系列答案
相关题目
已知双曲线x2-y2=a2（a＞0）的左、右顶点分别为A、B，双曲线在第一象限的图象上有一点P，∠PAB=α，∠PBA=β，∠APB=γ，则（ ）
| A、tanα+tanβ+tanγ=0 | B、tanα+tanβ-tanγ=0 | C、tanα+tanβ+2tanγ=0 | D、tanα+tanβ-2tanγ=0 |