题目内容
13. 已知函数f(x)=2sin2($\frac{π}{4}$x+$\frac{π}{4}$)
已知函数f(x)=2sin2($\frac{π}{4}$x+$\frac{π}{4}$)(Ⅰ)把f(x)解析式化为f(x)=Asin(ωx+φ)+b的形式,并用五点法作出函数f(x)在一个周期上的简图;
(Ⅱ)计算f(1)+f(2)+…+f(2016)的值.
分析 (Ⅰ)利用倍角公式和诱导公式对函数解析式进行化简,再利用正弦函数的五个关键点进行列表、描点、连线;
(Ⅱ)根据函数解析式先求出周期,再求出一个周期内的函数值的和,进而判断出2012与周期的关系,再求出式子和的值.
解答 解:(Ⅰ)$f(x)=2{sin^2}(\frac{π}{4}x+\frac{π}{4})=1-cos(\frac{π}{2}x+\frac{π}{2})=1+sin\frac{π}{2}x$.…4 分
列表得:
| x | 0 | 1 | 2 | 3 | 4 |
| $\frac{π}{2}x$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| $y=1+sin\frac{π}{2}x$ | 1 | 2 | 1 | 0 | 1 |
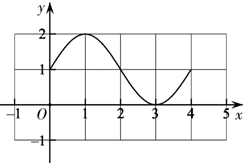
…(6分)
(Ⅱ)∵f(1)+f(2)+f(3)+f(4)=2+1+0+1=4.…(8分)
而y=f(x)的周期为4,
2016=4×504,
∴f(1)+f(2)+…+f(2016)=4×504=2016.…10 分
点评 本题是关于三角函数的综合题,涉及了倍角公式、诱导公式的应用,“五点作图法”的步骤,函数周期性的应用求式子的值,考查了分析、解决问题能力和作图能力.

练习册系列答案
相关题目
4.设F为抛物线y2=4x的焦点,直线l与其交于A,B两点,与x轴交于P点,且以AB为直径的圆过原点O,则$\overrightarrow{OF}•\overrightarrow{FP}$等于( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
18.在△ABC中,B=30°,C=60°,c=1,则最短边的边长等于( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
5.阅读如图所示的程序框图,当输入的值为3时,输出的结果是( )


| A. | 3 | B. | 8 | C. | 12 | D. | 20 |
2.不等式x>x2的解集是( )
| A. | {x|x<0} | B. | {x|x>0} | C. | {x|x<1} | D. | {x|0<x<1} |