题目内容
14.求函数f(x)=2sin(x+$\frac{π}{4}$)sin(x-$\frac{π}{4}$)+sin2x的最大值.分析 由条件利用三角恒等变换化简函数的解析式为y=$\sqrt{2}$sin(2x-$\frac{π}{4}$)≤$\sqrt{2}$,从而求得函数的最大值.
解答 解:函数f(x)=2sin(x+$\frac{π}{4}$)sin(x-$\frac{π}{4}$)+sin2x=2($\frac{\sqrt{2}}{2}$sinx+$\frac{\sqrt{2}}{2}$cosx)($\frac{\sqrt{2}}{2}$sinx-$\frac{\sqrt{2}}{2}$cosx)+sin2x
=-cos2x+sin2x=$\sqrt{2}$sin(2x-$\frac{π}{4}$)≤$\sqrt{2}$,
故函数的最大值为$\sqrt{2}$.
点评 本题主要考查利用三角恒等变换化简函数的解析式,正弦函数的值域,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知数列{an}为等差数列,若a3+a7=20,则数列{an}的前9项和S9等于( )
| A. | 40 | B. | 45 | C. | 60 | D. | 90 |
6.在($\sqrt{x}-\frac{2}{\sqrt{x}}$)n的展开式中,偶数项的二次项系数为64,则展开式共有( )
| A. | 6项 | B. | 7项 | C. | 8项 | D. | 9项 |
3.函数f(x)=3sin(2x-$\frac{π}{6}$),在区间[0,$\frac{π}{2}$]上的值域为( )
| A. | [-$\frac{3}{2}$,$\frac{3}{2}$] | B. | [-$\frac{3}{2}$,3] | C. | [-$\frac{3\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{2}$] | D. | [-$\frac{3\sqrt{3}}{2}$,3] |
17.若tanθ=2,则sin2θ+sinθcosθ-2cos2θ=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{7}}{4}$ | D. | $\frac{3}{4}$ |
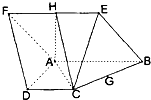 如图已知:菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H,G分别是线段EF,BC的中点.
如图已知:菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H,G分别是线段EF,BC的中点.