题目内容
 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.(I)证明:PB⊥CD;
(II)求二面角A-PD-C的大小.
分析:(I)取BC的中点E,连接DE,过点P作PO⊥平面ABCD于O,连接OA、OB、OD、OE.可证出四边形ABED是正方形,且O为正方形ABED的中心.因此OE⊥OB,结合三垂线定理,证出OE⊥PB,而OE是△BCD的中位线,可得OE∥CD,因此PB⊥CD;
(II)由(I)的结论,证出CD⊥平面PBD,从而得到CD⊥PD.取PD的中点F,PC的中点G,连接FG,可得FG∥CD,所以FG⊥PD.连接AF,可得AF⊥PD,因此∠AFG为二面角A-PD-C的平面角,连接AG、EG,则EG∥PB,可得EG⊥OE.设AB=2,可求出AE、EG、AG、AF和FG的长,最后在△AFG中利用余弦定理,算出∠AFG=π-arccos
,即得二面角A-PD-C的平面角大小.
(II)由(I)的结论,证出CD⊥平面PBD,从而得到CD⊥PD.取PD的中点F,PC的中点G,连接FG,可得FG∥CD,所以FG⊥PD.连接AF,可得AF⊥PD,因此∠AFG为二面角A-PD-C的平面角,连接AG、EG,则EG∥PB,可得EG⊥OE.设AB=2,可求出AE、EG、AG、AF和FG的长,最后在△AFG中利用余弦定理,算出∠AFG=π-arccos
| ||
| 3 |
解答: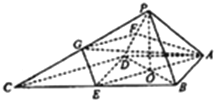 解:(I)取BC的中点E,连接DE,可得四边形ABED是正方形
解:(I)取BC的中点E,连接DE,可得四边形ABED是正方形
过点P作PO⊥平面ABCD,垂足为O,连接OA、OB、OD、OE
∵△PAB与△PAD都是等边三角形,∴PA=PB=PD,可得OA=OB=OD
因此,O是正方形ABED的对角线的交点,可得OE⊥OB
∵PO⊥平面ABCD,得直线OB是直线PB在内的射影,∴OE⊥PB
∵△BCD中,E、O分别为BC、BD的中点,∴OE∥CD,可得PB⊥CD;
(II)由(I)知CD⊥PO,CD⊥PB
∵PO、PB是平面PBD内的相交直线,∴CD⊥平面PBD
∵PD?平面PBD,∴CD⊥PD
取PD的中点F,PC的中点G,连接FG,
则FG为△PCD有中位线,∴FG∥CD,可得FG⊥PD
连接AF,由△PAD是等边三角形可得AF⊥PD,∴∠AFG为二面角A-PD-C的平面角
连接AG、EG,则EG∥PB
∵PB⊥OE,∴EG⊥OE,
设AB=2,则AE=2
,EG=
PB=1,故AG=
=3
在△AFG中,FG=
CD=
,AF=
,AG=3
∴cos∠AFG=
=-
,得∠AFG=π-arccos
,
即二面角A-PD-C的平面角大小是π-arccos
.
 解:(I)取BC的中点E,连接DE,可得四边形ABED是正方形
解:(I)取BC的中点E,连接DE,可得四边形ABED是正方形过点P作PO⊥平面ABCD,垂足为O,连接OA、OB、OD、OE
∵△PAB与△PAD都是等边三角形,∴PA=PB=PD,可得OA=OB=OD
因此,O是正方形ABED的对角线的交点,可得OE⊥OB
∵PO⊥平面ABCD,得直线OB是直线PB在内的射影,∴OE⊥PB
∵△BCD中,E、O分别为BC、BD的中点,∴OE∥CD,可得PB⊥CD;
(II)由(I)知CD⊥PO,CD⊥PB
∵PO、PB是平面PBD内的相交直线,∴CD⊥平面PBD
∵PD?平面PBD,∴CD⊥PD
取PD的中点F,PC的中点G,连接FG,
则FG为△PCD有中位线,∴FG∥CD,可得FG⊥PD
连接AF,由△PAD是等边三角形可得AF⊥PD,∴∠AFG为二面角A-PD-C的平面角
连接AG、EG,则EG∥PB
∵PB⊥OE,∴EG⊥OE,
设AB=2,则AE=2
| 2 |
| 1 |
| 2 |
| AE2+EG2 |
在△AFG中,FG=
| 1 |
| 2 |
| 2 |
| 3 |
∴cos∠AFG=
| 2+3-9 | ||||
2×
|
| ||
| 3 |
| ||
| 3 |
即二面角A-PD-C的平面角大小是π-arccos
| ||
| 3 |
点评:本题给出特殊的四棱锥,求证直线与直线垂直并求二面角平面角的大小,着重考查了线面垂直的判定与性质、三垂线定理和运用余弦定理求二面的大小等知识,属于中档题.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=