题目内容
18.由动点P向圆x2+y2=1引两条切线PA、PB,切点分别为A、B,若∠APB=120°,则动点P的轨迹方程为x2+y2=$\frac{4}{3}$.分析 根据切线的性质可得OP=$\frac{2\sqrt{3}}{3}$,从而得出P点的轨迹方程.
解答 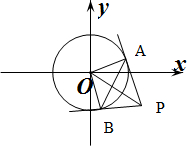 解:连接OP,AB,OA,OB,
解:连接OP,AB,OA,OB,
∵PA,PB是单位圆O的切线,
∴PA=PB,OA⊥PA,OB⊥PB,
∴∠OPA=∠OPB=$\frac{1}{2}$∠APB=60°,
又OA=OB=1,∴OP=$\frac{2\sqrt{3}}{3}$,
∴P点轨迹为以O为圆心,以$\frac{2\sqrt{3}}{3}$为半径的圆,
∴P点轨迹方程为x2+y2=$\frac{4}{3}$.
故答案为:x2+y2=$\frac{4}{3}$.
点评 本题考查了轨迹方程的求法,直线与圆的位置关系,属于中档题.

练习册系列答案
相关题目
9.下列说法中正确的是( )
| A. | 第一象限角一定是正角 | B. | 终边与始边均相同的角一定相等 | ||
| C. | -834°是第四象限角 | D. | 钝角一定是第二象限角 |