题目内容
设 ,
, 为两个不共线的向量,若
为两个不共线的向量,若 =
= ,
, ;
;
(1)若 、
、 共线,求λ值;
共线,求λ值;
(2)若 ,
, 为互相垂直的单位向量,求
为互相垂直的单位向量,求 、
、 垂直时λ的值.
垂直时λ的值.
解:(1)∵ 、
、 共线,∴设
共线,∴设 (m∈R)
(m∈R)
∵ =
= ,
, ;
;
∴
∴
∴λ=-
(2)∵ ,
, 为互相垂直的单位向量,
为互相垂直的单位向量,
∴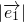 =1,
=1,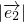 =1,
=1, =0
=0
∵ 、
、 垂直,∴
垂直,∴ =0
=0
∴ =0
=0
∴-2 +(3-2λ)
+(3-2λ) +3
+3 =0
=0
∴-2+3λ=0
∴λ=
分析:(1)由非零向量 、
、 共线的充要条件为存在实数m,使
共线的充要条件为存在实数m,使 ,将
,将 =
= ,
, 代入,得关于不共线的向量
代入,得关于不共线的向量 ,
, 的等式,由平面向量基本定理得方程,即可解得λ值
的等式,由平面向量基本定理得方程,即可解得λ值
(2)由向量 、
、 垂直的充要条件为
垂直的充要条件为 =0,将
=0,将 =
= ,
, 代入,得关于不共线的向量
代入,得关于不共线的向量 ,
, 的等式,因为
的等式,因为 ,
, 为互相垂直的单位向量,利用向量数量积运算性质即可得方程,解之即可
为互相垂直的单位向量,利用向量数量积运算性质即可得方程,解之即可
点评:本题考查了向量共线的充要条件,向量垂直的充要条件,平面向量基本定理,向量数量积运算及其性质
 、
、 共线,∴设
共线,∴设 (m∈R)
(m∈R)∵
 =
= ,
, ;
;∴

∴

∴λ=-

(2)∵
 ,
, 为互相垂直的单位向量,
为互相垂直的单位向量,∴
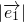 =1,
=1,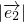 =1,
=1, =0
=0∵
 、
、 垂直,∴
垂直,∴ =0
=0∴
 =0
=0∴-2
 +(3-2λ)
+(3-2λ) +3
+3 =0
=0∴-2+3λ=0
∴λ=

分析:(1)由非零向量
 、
、 共线的充要条件为存在实数m,使
共线的充要条件为存在实数m,使 ,将
,将 =
= ,
, 代入,得关于不共线的向量
代入,得关于不共线的向量 ,
, 的等式,由平面向量基本定理得方程,即可解得λ值
的等式,由平面向量基本定理得方程,即可解得λ值(2)由向量
 、
、 垂直的充要条件为
垂直的充要条件为 =0,将
=0,将 =
= ,
, 代入,得关于不共线的向量
代入,得关于不共线的向量 ,
, 的等式,因为
的等式,因为 ,
, 为互相垂直的单位向量,利用向量数量积运算性质即可得方程,解之即可
为互相垂直的单位向量,利用向量数量积运算性质即可得方程,解之即可点评:本题考查了向量共线的充要条件,向量垂直的充要条件,平面向量基本定理,向量数量积运算及其性质

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 为两个不共线的向量,
为两个不共线的向量,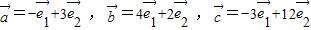 ,试用
,试用 为基底表示向量
为基底表示向量 ;
; ,当k为何值时,
,当k为何值时, ∥
∥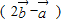 ?平行时它们是同向还是反向?
?平行时它们是同向还是反向?