Question

已知函数f(x)=

3

sinxcosx-cos2x+

1

2

，
（I）求函数f（x）的最小正周期；
（II）试用“五点法”做出函数f（x）在[

π

12

，

13π

12

]内的简图，并指出该函数可由函数y=sinx（x∈R）的图象经过怎样的先平移后伸缩变换得到．

Answer 1

分析：（I）由倍角公式和两角差的正弦公式化简解析式，再求出函数的周期；
（II）利用五点法，将2x-

π

6

看成整体取正弦函数的五个关键点，通过列表、描点、连线画出函数图象，用图象变换的方法得此函数图象，可以先向左平移，再横向伸缩，再向上平移的顺序进行．

解答：解：（I）由题意得，f(x)=

3

2

sin2x-

1+cos2x

2

+

1

2

=

3

2

sin2x-

1

2

cos2x=sin(2x-

π

6

)，
∴函数f（x）的最小正周期T=

2π

2

=π，
（II）列表如下：

x	π 12	π 3	7π 12	5π 6	13π 12
2x+ π 6	0	π 2	π	3π 2	2π
sin（2x+ π 6 ）	0	1	0	-1	0

画简图：

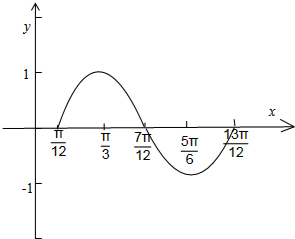
函数y=sinx的图象向右平移

π

6

个单位，再保持纵坐标不变，把横坐标缩短为原来的一半，
得到函数f(x)=sin(2x-

π

6

)的图象．

点评：本题综合考查了三角变换公式的运用，三角函数的图象画法：五点法和整体思想，三角函数图象变换法则，属于较综合的题目．