题目内容
直线 与圆
与圆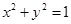 交于不同两点
交于不同两点 、
、 ,
, 为坐标原点,则“
为坐标原点,则“ ”是“向量
”是“向量 、
、 满足
满足 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:根据题意,由于直线 与圆
与圆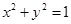 交于不同两点
交于不同两点 、
、 ,当a=1时,则可以利用圆心到直线的距离公式可知d=
,当a=1时,则可以利用圆心到直线的距离公式可知d= ,可知当a="1" 时,A(1,0),B(0,1),,可以得到
,可知当a="1" 时,A(1,0),B(0,1),,可以得到 ,当满足
,当满足 ,时a不一定等于1,如a=-1也可以,故必要性不成立,故选A.
,时a不一定等于1,如a=-1也可以,故必要性不成立,故选A.
考点:直线和圆的位置关系
点评:本题考查直线和圆的位置关系,充分条件、必要条件、充要条件的定义.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
将圆 平分的直线的方程可以是( )
平分的直线的方程可以是( )
A. | B. | C. | D. [ [ |
已知圆C经过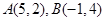
 两点,圆心在x轴上,则圆C的方程是
两点,圆心在x轴上,则圆C的方程是
A.  | B.  |
C.  | D. |
已知 , 点
, 点 是圆
是圆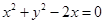 上的动点,则点M到直线AB的最大距离是
上的动点,则点M到直线AB的最大距离是
A. | B.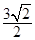 | C. | D. |
直线 与圆
与圆 交于
交于 、
、 两点,且
两点,且 、
、 关于直线
关于直线 对称,则弦
对称,则弦 的长为
的长为
| A. 2 | B.3 | C. 4 | D.5 |
已知直线 :
: 和圆C:
和圆C:  ,则直线
,则直线 和圆C的位置关系为( ).
和圆C的位置关系为( ).
| A.相交 | B.相切 | C.相离 | D.不能确定 |
在平面直角坐标系 中,直线
中,直线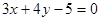 与圆
与圆 相交于
相交于 、
、 两点,则弦
两点,则弦 的长等于( )
的长等于( )
A.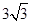 | B. | C. | D. |
圆 和
和 的位置关系是( )
的位置关系是( )
| A.相离 | B.外切 | C.相交 | D.内切 |



