题目内容
设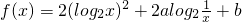 ,已知
,已知 时,f(x)有最小值-8.
时,f(x)有最小值-8.
(1)求a与b的值;
(2)在(1)的条件下,求f(x)>0的解集A;
(3)设集合 ,且A∩B=∅,求实数t的取值范围.
,且A∩B=∅,求实数t的取值范围.
(本小题满分13分)
解:(1)令 ,
,
t=log2x,y=2t2-2at+b,
由已知 ,即t=-1时,f(x)有最小值-8,
,即t=-1时,f(x)有最小值-8,
得二次函数的对称轴为 ,得a=-2,
,得a=-2,
 ,得b=-6;
,得b=-6;
即a与b的值分别为-2,-6;
(2)由a与b的值分别为-2,-6,
得 ,
,
即 ,
,
得log2x>1,或log2x<-3,
即x>2,或 ,
,
得集合 ;
;
(3)集合 ,而A∩B=∅,
,而A∩B=∅,
得 ,或
,或 ,
,
解得 ,或
,或 ,
,
即实数t的取值范围为 ,或
,或 .
.
分析:(1)令 ,t=log2x,y=2t2-2at+b,由
,t=log2x,y=2t2-2at+b,由 ,即t=-1时,f(x)有最小值-8,得二次函数的对称轴为
,即t=-1时,f(x)有最小值-8,得二次函数的对称轴为 ,得a=-2,由此能求出a与b的值.
,得a=-2,由此能求出a与b的值.
(2)由a与b的值分别为-2,-6,得 ,由此能求出f(x)>0的解集A.
,由此能求出f(x)>0的解集A.
(3)集合 ,而A∩B=∅,得
,而A∩B=∅,得 ,或
,或 ,由此能求出实数t的取值范围.
,由此能求出实数t的取值范围.
点评:本题考查二次函数的性质和应用,是中档题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
解:(1)令
 ,
,t=log2x,y=2t2-2at+b,
由已知
 ,即t=-1时,f(x)有最小值-8,
,即t=-1时,f(x)有最小值-8,得二次函数的对称轴为
 ,得a=-2,
,得a=-2, ,得b=-6;
,得b=-6;即a与b的值分别为-2,-6;
(2)由a与b的值分别为-2,-6,
得
 ,
,即
 ,
,得log2x>1,或log2x<-3,
即x>2,或
 ,
,得集合
 ;
;(3)集合
 ,而A∩B=∅,
,而A∩B=∅,得
 ,或
,或 ,
,解得
 ,或
,或 ,
,即实数t的取值范围为
 ,或
,或 .
.分析:(1)令
 ,t=log2x,y=2t2-2at+b,由
,t=log2x,y=2t2-2at+b,由 ,即t=-1时,f(x)有最小值-8,得二次函数的对称轴为
,即t=-1时,f(x)有最小值-8,得二次函数的对称轴为 ,得a=-2,由此能求出a与b的值.
,得a=-2,由此能求出a与b的值.(2)由a与b的值分别为-2,-6,得
 ,由此能求出f(x)>0的解集A.
,由此能求出f(x)>0的解集A.(3)集合
 ,而A∩B=∅,得
,而A∩B=∅,得 ,或
,或 ,由此能求出实数t的取值范围.
,由此能求出实数t的取值范围.点评:本题考查二次函数的性质和应用,是中档题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 ,已知
,已知 时,f(x)的最小值是-8.
时,f(x)的最小值是-8.
 ,已知
,已知 时,f(x)的最小值是-8.
时,f(x)的最小值是-8. ,已知
,已知 时,f(x)有最小值-8.
时,f(x)有最小值-8.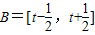 ,且A∩B=∅,求实数t的取值范围.
,且A∩B=∅,求实数t的取值范围.