题目内容
已知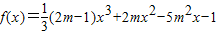 的极值点是-5,1.
的极值点是-5,1.(Ⅰ)求实数m的值;
(Ⅱ)求y=f(x)的递增区间.
【答案】分析:(Ⅰ)由函数极值的定义,先求函数f(x)的导函数,由f'(-5)=f'(1)=0,可得关于m的方程,解出即可;
(Ⅱ)在(1)的条件下f'(x)=x2+4x-5=(x+5)(x-1),解不等式f'(x)>0,即可得函数f(x)的单调递增区间.
解答:解:(Ⅰ)∵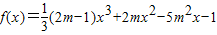 ,
,
∴f'(x)=(2m-1)x2+4mx-5m2
由题意,即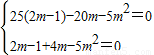 ,
,
解得,m=1.
经验证,当m=1时,f(x)的极值点是-5,1,所以m=1…6分
(Ⅱ)由(Ⅰ)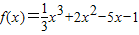 ,f'(x)=x2+4x-5=(x+5)(x-1),
,f'(x)=x2+4x-5=(x+5)(x-1),
解不等式f'(x)>0得,x<-5或x>1,
∴y=f(x)的递增区间是(-∞,-5],[1,+∞).…12分.
点评:本题综合考查了导数在函数极值、单调性中的应用,解题时要认真体会导数在研究函数性质方面的积极作用,规范解题.
(Ⅱ)在(1)的条件下f'(x)=x2+4x-5=(x+5)(x-1),解不等式f'(x)>0,即可得函数f(x)的单调递增区间.
解答:解:(Ⅰ)∵
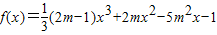 ,
,∴f'(x)=(2m-1)x2+4mx-5m2
由题意,即
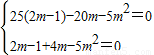 ,
,解得,m=1.
经验证,当m=1时,f(x)的极值点是-5,1,所以m=1…6分
(Ⅱ)由(Ⅰ)
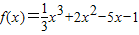 ,f'(x)=x2+4x-5=(x+5)(x-1),
,f'(x)=x2+4x-5=(x+5)(x-1),解不等式f'(x)>0得,x<-5或x>1,
∴y=f(x)的递增区间是(-∞,-5],[1,+∞).…12分.
点评:本题综合考查了导数在函数极值、单调性中的应用,解题时要认真体会导数在研究函数性质方面的积极作用,规范解题.

练习册系列答案
相关题目