题目内容
已知函数 是定义在R上的奇函数,
是定义在R上的奇函数, ,
,
 ,
,
则不等式  的解集是 .
的解集是 .
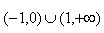
解析考点:利用导数研究函数的单调性.
分析:先根据 [ 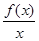 ]′=
]′=  >0判断函数
>0判断函数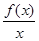 的单调性,进而分别看x>1和0<x<1时f(x)与0的关系.再根据函数的奇偶性判断-1<x<0和x<-1时f(x)与0的关系,最后去x的并集即可得到答案.
的单调性,进而分别看x>1和0<x<1时f(x)与0的关系.再根据函数的奇偶性判断-1<x<0和x<-1时f(x)与0的关系,最后去x的并集即可得到答案.
解:[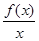 ]′=
]′= >0,即x>0时
>0,即x>0时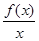 是增函数
是增函数
当x>1时,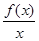 >f(1)=0,f(x)>0;
>f(1)=0,f(x)>0;
0<x<1时,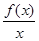 <f(1)=0,f(x)<0.
<f(1)=0,f(x)<0.
又f(x)是奇函数,所以-1<x<0时,f(x)=-f(-x)>0;x<-1时f(x)=-f(-x)<0.
则不等式f(x)>0的解集是(-1,0)∪(1,+∞)
故答案为:(-1,0)∪(1,+∞).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时不等式
时不等式 成立, 若
成立, 若 ,
,
 ,则
,则 的大小关系是 .
的大小关系是 . 是定义在R上的增函数,且
是定义在R上的增函数,且 ,则m的取值范围是
.
,则m的取值范围是
. 是定义在R上的奇函数,
是定义在R上的奇函数, ,
,
 ,
,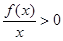 的解集是
.
的解集是
.