Question

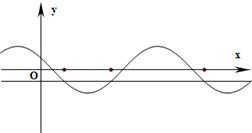已知函数f（x）=sin（ωx+?）（ω＞0，0＜φ＜π）的图象与直线y=b （-1＜b＜0）的三个相邻交点的横坐标分别是1，3，7．
（Ⅰ）求f（x）的解析式，并求x∈[0，1]时f（x）的值域；
（Ⅱ）试叙述y=f（x）的图象是由y=sinx的图象经怎样变换而得到．

Answer 1

分析：（Ⅰ）由题意求出T，然后求出ω，利用对称性，确定φ，求得f（x）的解析式，根据x∈[0，1]，求出

π

3

x+

5

6

π∈[

5

6

π，

7

6

π]，推出f（x）的值域；
（Ⅱ）y=f（x）的图象是由y=sinx的图象先向左平移，再横坐标缩短到原来的

3

π

倍而得到．也可以先缩短，后平移即可．

解答：解：（Ⅰ）依题意得：T=6∴ω=

π

3

即f(x)=sin(

π

3

x+φ)
又f（x）关于直线x=2对称
∴

2

3

π+φ=

π

2

+kπ，0＜φ＜π
∴φ=

5

6

π
∴f(x)=sin(

π

3

x+

5

6

π)，
若x∈[0，1]，则

π

3

x+

5

6

π∈[

5

6

π，

7

6

π]
∴f（x）的值域为[-

1

2

，

1

2

]
（Ⅱ）y=sinx的图象向左移

5

6

π得到y=sin(x+

5

6

π)；
再把该图象的横坐标缩短到原来的

3

π

倍（纵坐标不变）得到y=sin(

π

3

x+

5

6

π)

点评：本题考查函数y=Asin（ωx+φ）的图象变换，三角函数的周期性及其求法，正弦函数的定义域和值域，考查计算能力，是基础题．