题目内容
通过计算可得下列等式:22-12=2×1+1,
32-22=2×2+1,
42-32=2×3+1,
……
(n+1)2-n2=2n+1.
将以上各等式两边分别相加得(n+1)2-12=2(1+2+…+n)+n,即1+2+3+…+n=![]() .
.
(1)类比上述求法,请你求出12+22+32+…+n2的值.
(2)根据上述结论试求12+32+52+…+992的值.?
解:(1)∵23-13=3×12+3×1+1,?
33-23=3×22+3×2+1,?
43-33=3×32+3×3+1,?
……?
(n+1)3-n3=3×n2+3×n+1.?
将以上各式两边分别相加得?
(n+1)3-13=3(12+22+…+n2)+3(1+2+…+n)+n,?
∴12+22+…+n2?
=![]() [(n+1)3-1-n-3
[(n+1)3-1-n-3![]() n]?
n]?
=![]() n(n+1)(2n+1).?
n(n+1)(2n+1).?
(2)12+32+52+…+992=12+22+32+…+1002-(22+42+62+…+1002)?
=12+22+32+…+1002-4(12+22+32+…+502)?
=![]() ×100×101×201-4×
×100×101×201-4×![]() ×50×51×101?
×50×51×101?
=166 650.

练习册系列答案
相关题目
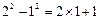 ,
,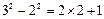 ,
,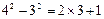 ,┅┅,
,┅┅,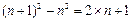
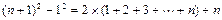
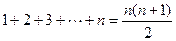
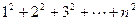 的值(要求必须有运算推理过程).
的值(要求必须有运算推理过程). ,
, ,
, ,┅┅,
,┅┅,


 的值(要求必须有运算推理过程).
的值(要求必须有运算推理过程).