题目内容
已知集合
，B={x|（x-a-1）（x-2a）＜0}，其中a＜1
（1）求集合A、B；
（2）若A∪B=A，求实数a的取值范围．
解：（1）2-
≥0，得
≥0，x＜-1或x≥1，即A=（-∞，-1）∪[1，+∞）．
由（x-a-1）（2a-x）＞0，得（x-a-1）（x-2a）＜0．
∵a＜1，∴a+1＞2a，∴B=（2a，a+1）．
（2）若A∪B=A，则有 B⊆A，∴2a≥1或a+1≤-1，即a≥
或a≤-2．
而a＜1，∴≤a＜1或a≤-2，
故当B⊆A时，实数a的取值范围是
．
分析：（1）解分式不等式求出集合A，解一元二次不等式求出集合B．
（2）由B⊆A，可得2a≥1或a+1≤-1，再由a＜1，求出实数a的取值范围．
点评：本题主要考查集合关系中参数的取值范围问题，一元二次不等式和分式不等式的解法，属于中档题．
≥0，得≥0，x＜-1或x≥1，即A=（-∞，-1）∪[1，+∞）．由（x-a-1）（2a-x）＞0，得（x-a-1）（x-2a）＜0．
∵a＜1，∴a+1＞2a，∴B=（2a，a+1）．
（2）若A∪B=A，则有 B⊆A，∴2a≥1或a+1≤-1，即a≥
或a≤-2．而a＜1，∴
≤a＜1或a≤-2，故当B⊆A时，实数a的取值范围是
．分析：（1）解分式不等式求出集合A，解一元二次不等式求出集合B．
（2）由B⊆A，可得2a≥1或a+1≤-1，再由a＜1，求出实数a的取值范围．
点评：本题主要考查集合关系中参数的取值范围问题，一元二次不等式和分式不等式的解法，属于中档题．
练习册系列答案
相关题目
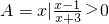，B={x|（x+3）（x-a2）≤0}．
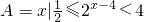，B={x|x2-11x+18＜0}．
，B={x|x2-11x+18＜0}．
，B={x|（x+a）（x-2a）≤0}，其中a＞0．
，B={x|m+1≤x≤3m-1}．