Question

（本小题满分10分）选修4—5：不等式选讲
已知函数，．
（1）解关于的不等式（）；
（2）若函数的图象恒在函数图象的上方，求的取值范围．

Answer 1

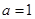(1) 当时，解集为；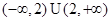
当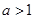时，解集为全体实数；
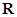当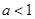时，解集为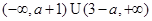 
(2)

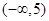
解析试题分析：（1）不等式即为，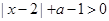
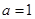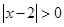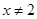当时，不等式变为，所以，即解集为；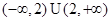
当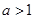时，解集为全体实数；
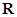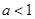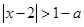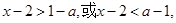当时，不等式变为，所以所以解集为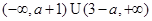.                                               ---5分
（2）的图象恒在函数图象的上方，
即为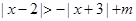对任意实数恒成立，
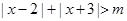即恒成立，
又对任意实数恒有，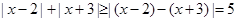
于是得，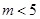
即的取值范围是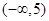.                                            ---10分
考点：本小题主要考查含绝对值的不等式的解法和利用绝对值的意义求不等式的最值从而解决不等式恒成立问题,考查学生分类讨论思想的应用.
点评：解含绝对值的不等式关键是讨论去掉绝对值号，要注意讨论时要做到不重不漏.