Question

（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
A．（不等式选做题）不等式|x+1|≥|x+2|的解集为    ．
B．（几何证明选做题）如图所示，过⊙O外一点P作一条直线与⊙O交于A，B两点，
已知PA=2，点P到⊙O的切线长PT=4，则弦AB的长为    ．
C．（坐标系与参数方程选做题）若直线3x+4y+m=0与圆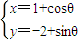（θ为参数）没有公共点，则实数m的取值范围是    ．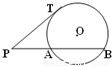

Answer 1

【答案】分析：A：根据a≥b≥0，则a²≥b²，将等式|x+1|≥|x+2|转化为一个整式不等式，解变形后的不等式即可得到答案；
B：利用切割线定理，我们易求出PB的长，进而求出AB的长；
C；由圆的参数方程，我们易判断出圆的圆心和半径，根据直线与圆的位置关系，我们易构造一个关于m的不等式，解不等式即可得到实数m的取值范围．
解答：解：A：不等式|x+1|≥|x+2|可化为
（x+1）²≥（x+2）²
即2x+1≥4x+4
解得x≤-
故不等式|x+1|≥|x+2|的解集为
故答案为：
B：由切割线定理可得：
PT²=PA•PB
∵PA=2，PT=4
∴PB=8
∴AB=6
故答案为：6
C：圆的圆心为（1，-2）半径为1
若直线3x+4y+m=0与圆（θ为参数）没有公共点
则表示圆心到直线的距离大于半径
即
即|m-5|＞5
解得m∈（-∞，0）∪（10，+∞）
故答案为：（-∞，0）∪（10，+∞）
点评：本题考查的知识点是与圆有关的比例线段，直线与圆的位置关系，圆的参数方程，绝对值不等式的解法．A中绝对值不等式的解法关键是要将不等式中的绝对值符号去掉；B中由已知利用切割线定理求出PB是关键；C中利用圆的参数方程求出圆的圆心坐标及半径是解答的关键．