题目内容
连掷两次骰子分别得到点数m,n,向量| a |
| b |
| 5 |
| 12 |
分析:由题意知本题是一个等可能事件的概率,试验发生包含的事件数36,满足条件的事件是使得向量的夹角是一个锐角,列举出所有的事件数,根据等可能事件的概率公式得到结果.
解答:解:由题意知本题是一个等可能事件的概率
∵向量
=(1,-1)
∴向量
的斜率是-1
∵夹角是一个锐角
∴向量
的斜率≤1
∵
>0是定义域
∴满足1>
>0 也就是n<m 进行列举:(2,1)(3,1)(4,1)
(5,1)(6,1)(3,2)(4,2)(5,2)(6,2)
(4,3)(5,3)(6,3)(5,4)(6,4)(6,5)共有15种
∴是锐角的概率是
=
故答案为:
∵向量
| b |
∴向量
| b |
∵夹角是一个锐角
∴向量
| a |
∵
| n |
| m |
∴满足1>
| n |
| m |
(5,1)(6,1)(3,2)(4,2)(5,2)(6,2)
(4,3)(5,3)(6,3)(5,4)(6,4)(6,5)共有15种
∴是锐角的概率是
| 15 |
| 36 |
| 5 |
| 12 |
故答案为:
| 5 |
| 12 |
点评:本题考查等可能事件的概率,考查向量的夹角,是一个简单的综合题,把向量同等可能事件结合起来,是一个只要细心就能得分的题目.

练习册系列答案
相关题目
先后连掷两次骰子分别得到点数m,n,则向量(m,n)与向量(-1,1)的夹角θ>90°的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 与向量
与向量 的夹角为
的夹角为 ,则
,则 的概率是( )
的概率是( )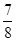 B.
B. C.
C. D.
D.