题目内容
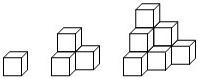
 将棱长相等的正方体按如图所示的形状摆放,从上往下依次为第一层、第二层、第三层…,则第2004层正方体的个数是( )
将棱长相等的正方体按如图所示的形状摆放,从上往下依次为第一层、第二层、第三层…,则第2004层正方体的个数是( )分析:观察可得,第1层正方体的个数为1,第2层正方体的个数为3,比第1层多2个,第3层正方体的个数为6,比第2层多3个;…可得,每一层比上一层多的个数依次为2,3,4,5,…,从而可求出第2004层正方体的个数.
解答:解:观察可得,第1层正方体的个数为1,第2层正方体的个数为3,比第1层多2个;第3层正方体的个数为6,比第2层多3个;…
可得,每一层比上一层多的个数依次为2,3,4,5,…;
故第2004层正方体的个数1+2+3+4+…+2004=
=2009010.
故选A
可得,每一层比上一层多的个数依次为2,3,4,5,…;
故第2004层正方体的个数1+2+3+4+…+2004=
| (1+2004)×2004 |
| 2 |
故选A
点评:本题主要考查了平面图形的有规律变化,要求学生通过观察图形,分析、归纳发现其中的规律,并应用规律解决问题,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 将棱长相等的正方体按如右图所示的形状摆放,从上往下依次为第1层,第2层,第3层….则第2005层正方体的个数是( )
将棱长相等的正方体按如右图所示的形状摆放,从上往下依次为第1层,第2层,第3层….则第2005层正方体的个数是( )| A、4011 | B、4009 | C、2011015 | D、2009010 |
 将棱长相等的正方体按图所示的形状摆放,从上往下依次为第1层,第2层,第3层,…,则第6层正方体的个数是
将棱长相等的正方体按图所示的形状摆放,从上往下依次为第1层,第2层,第3层,…,则第6层正方体的个数是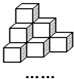 (2008•南汇区二模)将棱长相等的正方体按如图所示的形状摆放,从上往下依次为第1层、第2层、第3层、….则第2008层正方体的个数是
(2008•南汇区二模)将棱长相等的正方体按如图所示的形状摆放,从上往下依次为第1层、第2层、第3层、….则第2008层正方体的个数是