题目内容
已知正项数列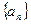 的前
的前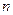 项和
项和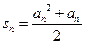 ,
,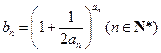 .
.
(Ⅰ)求数列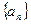 的通项公式;
的通项公式;
(Ⅱ)定理:若函数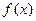 在区间D上是凹函数,且
在区间D上是凹函数,且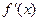 存在,则当
存在,则当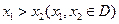 时,总有
时,总有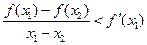 .请根据上述定理,且已知函数
.请根据上述定理,且已知函数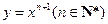 是
是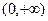 上的凹函数,判断
上的凹函数,判断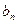 与
与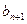 的大小;
的大小;
(Ⅲ)求证: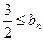 .
.
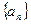 的前
的前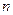 项和
项和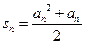 ,
,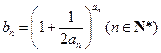 .
.(Ⅰ)求数列
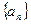 的通项公式;
的通项公式;(Ⅱ)定理:若函数
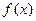 在区间D上是凹函数,且
在区间D上是凹函数,且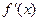 存在,则当
存在,则当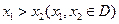 时,总有
时,总有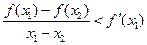 .请根据上述定理,且已知函数
.请根据上述定理,且已知函数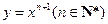 是
是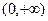 上的凹函数,判断
上的凹函数,判断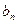 与
与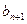 的大小;
的大小;(Ⅲ)求证:
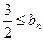 .
.(Ⅰ)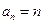 (
(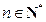 ).
).
(Ⅱ)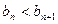 .
.
(Ⅲ)由(Ⅱ),得 .
.
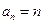 (
(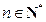 ).
). (Ⅱ)
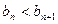 .
. (Ⅲ)由(Ⅱ),得
 .
.(Ⅰ)
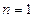 时,
时,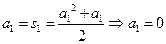 或
或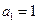 .
.由于
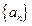 是正项数列,所以
是正项数列,所以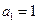 .
.当
 时,
时,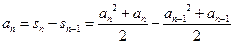 ,
, 整理,得
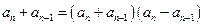 .
.由于
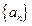 是正项数列,∴
是正项数列,∴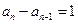 .
.∴数列
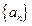 是以1为首项,1为公差的等差数列.
是以1为首项,1为公差的等差数列. 从而
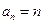 ,当
,当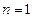 时也满足.
时也满足.∴
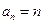 (
(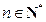 ).
). (Ⅱ)由(Ⅰ)知
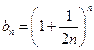 .
.对于
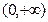 上的凹函数
上的凹函数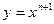 ,有
,有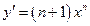 .
.根据定理,得
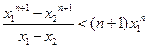 .
. 整理,得
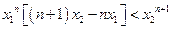 .
.令
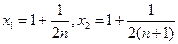 ,得
,得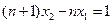 .
. ∴
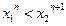 ,即
,即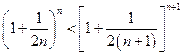 .
.∴
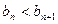 .
. (Ⅲ)由(Ⅱ),得
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
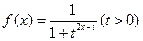 .
.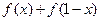 为定值;
为定值;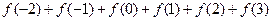 的值.
的值.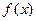 是定义在
是定义在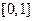 上的函数,若存在
上的函数,若存在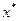
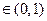 ,使得
,使得 上单调递增,在
上单调递增,在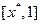 上单调递减,则称
上单调递减,则称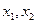
 ,若
,若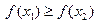 ,则
,则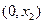 为含峰区间;若
为含峰区间;若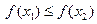 ,则
,则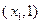 为含峰区间;
为含峰区间; ,证明:存在
,证明:存在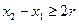 ,使得由(1)所确定的含峰区间的长度不大于
,使得由(1)所确定的含峰区间的长度不大于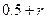 ;
;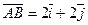 (
(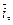
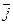 分别是与x轴和y轴正半轴同方向的单位向量),函数g(x)=
分别是与x轴和y轴正半轴同方向的单位向量),函数g(x)=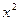 ―x―6,
―x―6,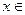 M时,求函数
M时,求函数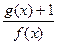 的最小值
的最小值 ,
, ,3].
,3]. ;
; .
.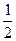 )的值;
)的值;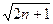 .(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
.(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.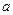
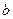
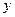 (元)表示为里程
(元)表示为里程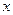 (km)的函数
(km)的函数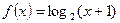 ,当点
,当点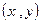 在函数
在函数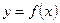 的图象上时,点
的图象上时,点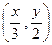 在函数
在函数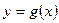 的图象上。
的图象上。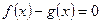 方程的根
方程的根