题目内容
已知函数 ,其中
,其中 R.
R.
(Ⅰ)若曲线 在点
在点 处的切线方程为
处的切线方程为 ,求函数
,求函数 的解析式;
的解析式;
(Ⅱ)当 时,讨论函数
时,讨论函数 的单调性.
的单调性.
【答案】
解:(Ⅰ)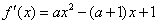 , ------------1分
, ------------1分
由导数的几何意义得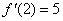 ,于是
,于是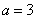 .
-----------------3分
.
-----------------3分
由切点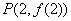 在直线
在直线 上可知
上可知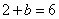 ,解得
,解得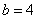 . -----5分
. -----5分
所以函数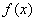 的解析式为
的解析式为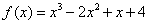 . ------------6分
. ------------6分
(Ⅱ) , ------------------7分
, ------------------7分
当 时,
时,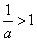 ,函数
,函数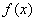 在区间
在区间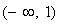 及
及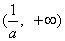 上为增函数;
上为增函数;
在区间 上为减函数;
--------------------------------------------------------9分
上为减函数;
--------------------------------------------------------9分
当 时,
时,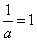 ,函数
,函数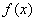 在区间
在区间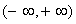 上为增函数;------------------10分
上为增函数;------------------10分
当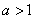 时,
时, ,函数
,函数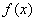 在区间
在区间 及
及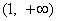 上为增函数;
上为增函数;
在区间 上为减函数.
--------------------------12分
上为减函数.
--------------------------12分
命题意图:本题考查了导数的几何意义、利用导数求函数的单调区间的方法以及分类讨论的数学思想。

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
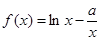 ,
,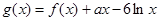 ,其中
,其中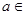 R.
R. 的单调性;
的单调性;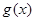 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围; ,当
,当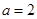 时,若
时,若 ,
,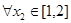 ,总有
,总有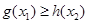 成立,求实数
成立,求实数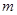 的取值范围.
的取值范围. ,
,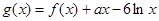 ,其中
,其中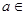 R.
R.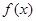 的单调性;
的单调性;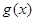 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数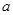 的取值范围;
的取值范围;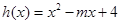 ,当
,当 时,若
时,若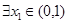 ,
,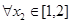 ,总有
,总有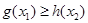 成立,求实数
成立,求实数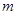 的取值范围.
的取值范围. ,
,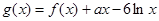 ,其中
,其中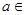 R
R 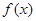 的单调性
的单调性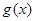 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数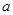 的取值范围
的取值范围 , 当
, 当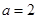 时,若
时,若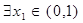 ,
,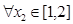 ,总有
,总有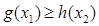 成立,求实数
成立,求实数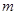 的取值范围
的取值范围 ,
,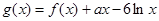 ,其中
,其中 R.
R. 的单调性;
的单调性;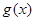 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数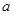 的取值范围;
的取值范围; ,当
,当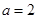 时,若
时,若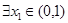 ,
, ,总有
,总有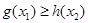 成立,求实数
成立,求实数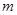 的取值范围
的取值范围