题目内容
直线y=kx+1与曲线y=x2+ax+b相切于点A（1，3），则a-b=（ ）
| A．-4 | B．-1 | C．3 | D．-2 |
∵y=x2+ax+b，∴y′=2x+a，k=f′（1）=2+a，
∵直线y=kx+1与曲线y=x2+ax+b相切于点A（1，3），
∴
，
解得k=2，a=0，b=2，
∴a-b=0-2=-2．
故选D．
∵直线y=kx+1与曲线y=x2+ax+b相切于点A（1，3），
∴
|
解得k=2，a=0，b=2，
∴a-b=0-2=-2．
故选D．
练习册系列答案
相关题目
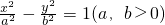的虚轴长为2
，渐近线方程是y=
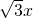，O为坐标原点，直线y=kx+m（k，m∈R）与双曲线C相交于A、B两点，且
．
的虚轴长为2
，渐近线方程是y=
，O为坐标原点，直线y=kx+m（k，m∈R）与双曲线C相交于A、B两点，且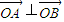
．