题目内容
等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2a6
(1)求数列{an}的通项公式.
(2)求数列{
}的前n项和Sn;
(3)设 bn=log
a3+…+log
a2n-1(n∈N*),若数列{bn+kn)是递增的数列,求k的取值范围..
(1)求数列{an}的通项公式.
(2)求数列{
| n |
| an |
(3)设 bn=log
| 1 |
| 3 |
| 1 |
| 3 |
分析:(1)设数列{an}的公比为q,通过解方程组可求得a1与q,从而可求数列{an}的通项公式;
(2)根据(1)的答案代入
得到表达式,然后利用错位相减法求出前n项和即可.
(3)先说明{bn}是一个首项为1,公差为2的等差数列,然后求出通项,再根据数列{bn+kn)是递增的数列建立关系式,解之即可.
(2)根据(1)的答案代入
| n |
| an |
(3)先说明{bn}是一个首项为1,公差为2的等差数列,然后求出通项,再根据数列{bn+kn)是递增的数列建立关系式,解之即可.
解答:解:(1)设数列{an}的公比为q,则根据已知条件得
2a1+3a2=2a1+3a1q=1,(a1q2)2=9a1q•a1q5
解得,q2=
,根据已知条件q>0,∴q=
,a1=
,
故数列{an}的通项式为an=
,
(2)
=n•3n,∴Sn=1•31+2•32+…+n•3n ①
3Sn=1•32+2•33+…+(n-1)•3n+n•3n+1 ②
②-①得,2Sn=-(31+32+…+3n)+n•3n+1+n•3n+1=
-(n+
)3n+1
∴Sn=
-
•3n+1
(3)a2n-1=
,∴log
a2n-1=log
=2n-1,
∴{bn}是一个首项为1,公差为2的等差数列,
bn=log
a3+…+log
a2n-1=
=n2
∴bn+kn=n2+kn,
又数列{bn+kn)是递增的数列,
∴-
≤
,解得k≥-3.
∴k的取值范围为k≥-3.
2a1+3a2=2a1+3a1q=1,(a1q2)2=9a1q•a1q5
解得,q2=
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 3 |
故数列{an}的通项式为an=
| 1 |
| 3n |
(2)
| n |
| an |
3Sn=1•32+2•33+…+(n-1)•3n+n•3n+1 ②
②-①得,2Sn=-(31+32+…+3n)+n•3n+1+n•3n+1=
| 3 |
| 2 |
| 1 |
| 2 |
∴Sn=
| 3 |
| 4 |
| 2n+1 |
| 4 |
(3)a2n-1=
| 1 |
| 32n-1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 32n-1 |
∴{bn}是一个首项为1,公差为2的等差数列,
bn=log
| 1 |
| 3 |
| 1 |
| 3 |
| n(1+2n-1) |
| 2 |
∴bn+kn=n2+kn,
又数列{bn+kn)是递增的数列,
∴-
| k |
| 2 |
| 3 |
| 2 |
∴k的取值范围为k≥-3.
点评:本题考查数列与不等式的综合以及数列求和,考查恒成立问题,考查学生分析解决问题的能力,属于中档题目.

练习册系列答案
相关题目
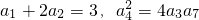 ,则数列{an}的通项公式为________.
,则数列{an}的通项公式为________. ,则数列{an}的通项公式为 .
,则数列{an}的通项公式为 .