题目内容
对于一个有n项的数列P=(P1,P2,…,Pn),P的“蔡查罗和”定义为
(S1+S2+…+Sn)其中Sk=(P1+P2+…+Pn)(1≤k≤n)若一个100项的数列(P1,P2,…,P100)的“蔡查罗和”为201.97,那么102项数列(1,1,P1,P2,…,P100)的“蔡查罗和”为
| 1 | n |
200
200
.分析:由“蔡查罗和”定义{P1,P2,P100}的“蔡查罗和”为
=201.97,故S1+S2+…+S100=20197,由此可推导出102项的数列{1,1,P1,P2,…,P100}“蔡查罗和”.
| S1+S2+…+S100 |
| 100 |
解答:解:由“蔡查罗和”定义,
{P1,P2,P100}的“蔡查罗和”为
=201.97,
∴S1+S2+…+S100=20197,
则102项的数列{1,1,P1,P2,…,P100}“蔡查罗和”为:
=
=200.
故答案为:200.
{P1,P2,P100}的“蔡查罗和”为
| S1+S2+…+S100 |
| 100 |
∴S1+S2+…+S100=20197,
则102项的数列{1,1,P1,P2,…,P100}“蔡查罗和”为:
| 1+2+(2+S1)+(2+S2)+…+(2+S100) |
| 102 |
=
| 1+2+200+20197 |
| 102 |
故答案为:200.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细求解.注意合理地进行等价转化.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 数列.对于
数列.对于 是否是关于(1,2,3,…,n)的万能数列,并证明你的结论.
是否是关于(1,2,3,…,n)的万能数列,并证明你的结论.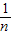 (S1+S2+…+Sn)其中Sk=(P1+P2+…+Pn)(1≤k≤n)若一个100项的数列(P1,P2,…,P100)的“蔡查罗和”为201.97,那么102项数列(1,1,P1,P2,…,P100)的“蔡查罗和”为 .
(S1+S2+…+Sn)其中Sk=(P1+P2+…+Pn)(1≤k≤n)若一个100项的数列(P1,P2,…,P100)的“蔡查罗和”为201.97,那么102项数列(1,1,P1,P2,…,P100)的“蔡查罗和”为 .