题目内容
函数y=
的单调减区间是 ．
【答案】分析：先化简函数的表达式，求函数的定义域，然后利用复合函数的单调性，求出函数的单调减区间即可．
解答：解：函数y=
=
，函数的定义域为：[kπ，kπ+
]（k∈Z），
因为 2kπ+
≤2x≤2kπ+π，
所以函数y=
的单调减区间是：[kπ+
，kπ+
]（k∈Z）
故答案为：[kπ+
，kπ+
]（k∈Z）．
点评：本题是基础题，考查正弦函数的单调性，函数的定义域，复合函数的单调性，是常考题，易错题．
解答：解：函数y=
=，函数的定义域为：[kπ，kπ+]（k∈Z），因为 2kπ+
≤2x≤2kπ+π，所以函数y=
的单调减区间是：[kπ+，kπ+]（k∈Z）故答案为：[kπ+
，kπ+]（k∈Z）．点评：本题是基础题，考查正弦函数的单调性，函数的定义域，复合函数的单调性，是常考题，易错题．
练习册系列答案
全能闯关100分系列答案
相关题目
的单调减区间是( ) 
，+∞） D.（-∞，
]
的单调减区间为_____________.
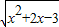的单调减区间是（-∞，-1）
的单调减区间是 ．