题目内容
设函数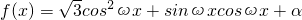 (其中ω>0,α∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为
(其中ω>0,α∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为 .
.
(I)求ω的值.
(II)如果f(x)在区间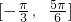 上的最小值为
上的最小值为 ,求α的值.
,求α的值.
解:(I)f(x)= cos2ωx+
cos2ωx+ sin2ωx+
sin2ωx+ +α
+α
=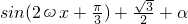
依题意得2ω× +
+ =
=
解之得ω=
(II)由(I)知f(x)=sin(x+ )+
)+ +α
+α
又当x∈[- ,
, ]时,x+
]时,x+ ∈[0,
∈[0, ]
]
故- ≤sin(x+
≤sin(x+ )≤1,
)≤1,
从而,f(x)在[- ,
, ]上取得最小值-
]上取得最小值- +
+ +α
+α
因此,由题设知- +
+ +α=
+α=
解得α=
答:(I)ω= ;(II)α=
;(II)α=
分析:(I)先用三角恒等式将函数f(x)表达式化简,再将最高点的坐标代入即可求出ω的值.
(II)利用三角函数的性质求出f(x)在区间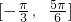 上的最小值表达式,令其值为
上的最小值表达式,令其值为 ,即可解出参数的值.
,即可解出参数的值.
点评:考查三角函数的图象与性质,先用性质求参数的值,再由函数的单调性判断出函数的最小值的参数表达式,建立关于参数的方程,求出相应的参数.本题可以培养答题者运用知识灵活转化的能力.
 cos2ωx+
cos2ωx+ sin2ωx+
sin2ωx+ +α
+α=
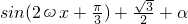
依题意得2ω×
 +
+ =
=
解之得ω=

(II)由(I)知f(x)=sin(x+
 )+
)+ +α
+α又当x∈[-
 ,
, ]时,x+
]时,x+ ∈[0,
∈[0, ]
]故-
 ≤sin(x+
≤sin(x+ )≤1,
)≤1,从而,f(x)在[-
 ,
, ]上取得最小值-
]上取得最小值- +
+ +α
+α因此,由题设知-
 +
+ +α=
+α=
解得α=

答:(I)ω=
 ;(II)α=
;(II)α=
分析:(I)先用三角恒等式将函数f(x)表达式化简,再将最高点的坐标代入即可求出ω的值.
(II)利用三角函数的性质求出f(x)在区间
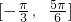 上的最小值表达式,令其值为
上的最小值表达式,令其值为 ,即可解出参数的值.
,即可解出参数的值.点评:考查三角函数的图象与性质,先用性质求参数的值,再由函数的单调性判断出函数的最小值的参数表达式,建立关于参数的方程,求出相应的参数.本题可以培养答题者运用知识灵活转化的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
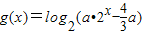 ,其中a>0.若函数f(x)与g(x)的图象有且只有一个交点,求a的取值范围.
,其中a>0.若函数f(x)与g(x)的图象有且只有一个交点,求a的取值范围. ,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2. (其中常数
(其中常数 >0,且
>0,且 时,解关于
时,解关于 的方程
的方程 (其中常数
(其中常数 );
); 在
在 上的最小值是一个与
上的最小值是一个与