题目内容
已知各项都不相等的等差数列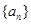 的前6项和为60,且
的前6项和为60,且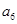 为
为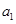 和
和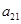 的等比中项.
的等比中项.
( I ) 求数列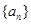 的通项公式;
的通项公式;
(II) 若数列 满足
满足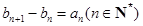 ,且
,且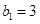 ,求数列
,求数列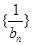 的前
的前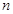 项和
项和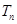 .
.
(1) (2)
(2)
解析试题分析:(1)根据已知条件列出关于首项a1和公差d的方程组,解出首项a1和公差d的值,即可求出等差数列的通项公式.(2)由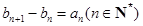 可得
可得 ,所以可推出
,所以可推出 ,即
,即 ,最后利用裂项法求解即可.
,最后利用裂项法求解即可.
试题解析:解:(Ⅰ)设等差数列 的公差为
的公差为 (
( ),
),
则 得
得 ∴
∴
(Ⅱ)由 , ∴
, ∴
 ,
,

 .
.
∴
 ∴
∴


考点:1.等差数列的通项公式和前n项和;2.等比中项;3.数列的递推公式和前n项和的求法.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
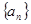 是递增的等差数列,且
是递增的等差数列,且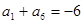 ,
,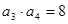 .
. 项和
项和 的最小值;
的最小值;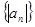 的前
的前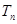 .
. 具有性质:①
具有性质:①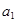 为正数;②对于任意的正整数
为正数;②对于任意的正整数 ,当
,当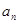 为偶数时,
为偶数时, ;当
;当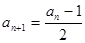
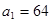 ,求数列
,求数列 成等差数列,求
成等差数列,求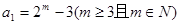 ,数列
,数列 ,求证:
,求证:
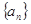 中,
中,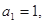 且点
且点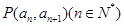 在直线
在直线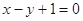 上。
上。 的通项公式;
的通项公式;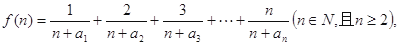 求函数
求函数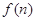 的最小值;
的最小值;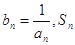 表示数列
表示数列 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于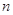 的整式
的整式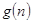 ,使得
,使得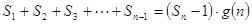 对于一切不小于2的自然数
对于一切不小于2的自然数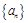 中,
中,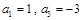 .
.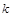 项和
项和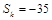 ,求
,求 时,其前n项和满足
时,其前n项和满足 .
. ,数列{bn}的前n项和为
,数列{bn}的前n项和为 ,求
,求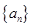 中,
中,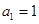 ,
, ,数列
,数列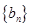 中,
中, ,且点
,且点 在直线
在直线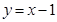 上.
上.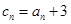 ,求数列
,求数列 的前项和
的前项和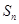 .
. 的首项为
的首项为 ,公比为
,公比为 (
( 是
是 与
与 的等差中项;数列
的等差中项;数列 满足
满足 (
( ).
). 的值,使得数列
的值,使得数列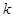 ,在
,在 与
与 之间插入
之间插入 个2,得到一个新数列
个2,得到一个新数列 . 设
. 设 是数列
是数列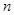 项和,试求满足
项和,试求满足 的所有正整数
的所有正整数 .
.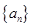 满足
满足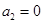 ,
,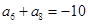 .
.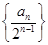 的前n项和.
的前n项和.