题目内容

如图，直三棱柱ABC—A1B1C1中，∠ACB=90°,AC=1,CB=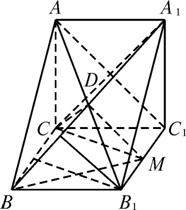,侧棱AA1=1，侧面AA1B1B的两条对角线交点为D，B1C1的中点为M.

求证：CD⊥平面BDM；

解析：本题主要考查线面关系和直棱柱等基础知识，同时考查空间想象能力和推理运算能力.

解：如图，连结CA1、AC1、CM，则CA1=.

∵CB=CA1=，∴△CBA1为等腰三角形.

又知D为其底边A1B的中点，∴CD⊥A1B.

∵A1C1=1,C1B1=,∴A1B1=.

又BB1=1，A1B=2，

△A1CB为直角三角形，D为A1B的中点.

∴CD=A1B=1,CD=CC1.

又DM=AC1=，DM=C1M，

∴△CDM≌△CC1M，∠CDM=∠CC1M=90°，即CD⊥DM.

∵A1B、DM为平面BDM内两条相交直线，∴CD⊥平面BDM.

练习册系列答案
相关题目
精英家教网如图，直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=1，CB=
2
，侧棱AA1=1，侧面AA1B1B的两条对角线交于点D，B1C1的中点为M，求证：CD⊥平面BDM．
精英家教网如图，直三棱柱ABC-A1B1C1中，底面是以∠ABC为直角的等腰直角三角形，AC=2a，BB1=3a，D为A1C1的中点，E为B1C的中点．
（1）求直线BE与A1C所成的角；
（2）在线段AA1中上是否存在点F，使CF⊥平面B1DF，若存在，求出|
AF
|；若不存在，说明理由．
精英家教网如图在直三棱柱ABC-A1B1C1中∠ACB=90°，AA1=2，AC=BC=1，则异面直线A1B与AC所成角的余弦值是
 
．
如图，直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=CC1=2，M，N分别为AC，B1C1的中点．
（Ⅰ）求线段MN的长；
（Ⅱ）求证：MN∥平面ABB1A1；
（Ⅲ）线段CC1上是否存在点Q，使A1B⊥平面MNQ？说明理由．
精英家教网如图，直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=a，AA1=2a，D棱B1B的中点．
（Ⅰ）证明：A1C1∥平面ACD；
（Ⅱ）求异面直线AC与A1D所成角的大小；
（Ⅲ）证明：直线A1D⊥平面ADC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网