题目内容
已知![]() 是定义在
是定义在![]() 上的函数,其图象与
上的函数,其图象与![]() 轴交于
轴交于![]() 三点,若
三点,若![]() 点的坐标为
点的坐标为![]() 且
且![]() 在
在![]() 和
和![]() 上有相同的单调性,在
上有相同的单调性,在![]() 和
和![]() 上有相反的单调性.(1)求
上有相反的单调性.(1)求![]() 的值;(2)在函数
的值;(2)在函数![]() 的图象上是否存在一点
的图象上是否存在一点![]() ,使得
,使得![]() 在点
在点![]() 的切线斜率为
的切线斜率为![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(1)![]()
解析:
(1)![]()
![]() 在
在![]() 和
和![]() 上有相反的单调性,
上有相反的单调性, ![]()
![]()
有一个解![]()
![]()
![]()
(2)令![]() 得
得 ![]()
![]()
![]() 在
在![]() 和
和![]() 上有相反的单调性,
上有相反的单调性, ![]()

![]()
![]() 假设存在一点
假设存在一点![]() ,使得
,使得![]() 在点
在点![]() 的切线斜率为
的切线斜率为![]() ,
,
即![]()
![]()
![]()
![]()
![]()
而![]() ,
,![]()
![]()
故不存在一点![]() ,使得
,使得![]() 在点
在点![]() 的切线斜率为
的切线斜率为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是定义在
是定义在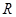 上的函数,
上的函数,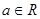 ,那么“对任意的
,那么“对任意的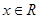 ,
,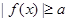 恒成立”的充要条件是( )
恒成立”的充要条件是( )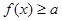 或
或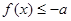 恒成立
恒成立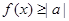 或
或 恒成立
恒成立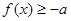 恒成立
恒成立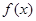 是定义在
是定义在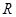 上的函数,且满足
上的函数,且满足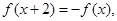 当
当 时,
时, ,则
,则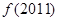 等于 A.
等于 A.
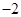 B.2 C.
B.2 C. 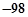 D.
98
D.
98 是定义在
是定义在 上的函数,对任意
上的函数,对任意 都有
都有 ,若函数
,若函数 的图象关于直线
的图象关于直线 对称,且
对称,且 ,则
,则 等于
等于