题目内容
19.设a=sin33°,b=cos58°,c=tan34°,则( )| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | c>a>b |
分析 可得b=sin32°,易得a>b,c=tan34°=$\frac{sin34°}{cos34°}$>sin34°>sin33°,综合可得答案.
解答 解:由诱导公式可得b=cos58°=cos(90°-38°)=sin32°,
由正弦函数的单调性可知a>b,
而c=tan34°=$\frac{sin34°}{cos34°}$>sin34°>sin33°=a,
∴c>a>b,
故选:D
点评 本题考查三角函数值大小的比较,涉及诱导公式和三角函数的单调性,属基础题.

练习册系列答案
相关题目
13.执行如图所示的程序框图,若输入x的值为2+log23,则输出y的值为( )
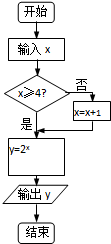

| A. | $\frac{8}{3}$ | B. | 8 | C. | 12 | D. | 24 |