题目内容
已知函数y=f(x)是定义在R上的奇函数,且当x∈(-∞,0)时,不等式f(x)+xf′(x)>0恒成立,若a=20.3f(20.3),b=(logπ2)f(logπ2),c=(log2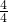 )f(log2
)f(log2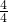 ),则a、b、c的大小关系是
),则a、b、c的大小关系是
- A.a>b>c
- B.c>b>a
- C.b>a>c
- D.a>c>b
A
分析:先确定xf(x)在 (0,+∞)上是增函数,再确定变量的大小关系,即可得到结论.
解答:∵当x∈(-∞,0)时不等式f(x)+xf′(x)<0成立,
∴(xf(x))′<0,
∴xf(x)在 (-∞,0)上是减函数.
又∵函数y=f(x)是定义在R上的奇函数,
∴xf(x)是定义在R上的偶函数,
∴xf(x)在 (0,+∞)上是增函数.
∵20.3>1>logπ2>log2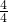
∴a>b>c
故选A.
点评:本题考查导数知识的运用,考查由已知函数构造新函数用原函数的性质来研究新函数,属于中档题.
分析:先确定xf(x)在 (0,+∞)上是增函数,再确定变量的大小关系,即可得到结论.
解答:∵当x∈(-∞,0)时不等式f(x)+xf′(x)<0成立,
∴(xf(x))′<0,
∴xf(x)在 (-∞,0)上是减函数.
又∵函数y=f(x)是定义在R上的奇函数,
∴xf(x)是定义在R上的偶函数,
∴xf(x)在 (0,+∞)上是增函数.
∵20.3>1>logπ2>log2
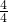
∴a>b>c
故选A.
点评:本题考查导数知识的运用,考查由已知函数构造新函数用原函数的性质来研究新函数,属于中档题.

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足