题目内容
已知等差数列{an}的公差为d(d≠0),等比数列{bn}的公比为q(q>1),设Sn=a1b1+a2b2+…anbn,Tn=a1b1-a2b2+…+(-1)n-1anbn,n∈N*。
(1)若a1=b1=1,d=2,q=3,求S3的值。
(2)若b1=1,证明:(1-q)S2n-(1+q)T2n=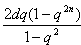 ,n∈N*。
,n∈N*。
(3)若正整数n满足2≤n≤q,设k1,k2,…kn和l1,l2,…ln是1,2,…,n的两个不同的排列,c1=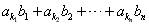 ,c2=
,c2=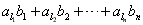 ,证明c1≠c2。
,证明c1≠c2。
(1)若a1=b1=1,d=2,q=3,求S3的值。
(2)若b1=1,证明:(1-q)S2n-(1+q)T2n=
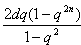 ,n∈N*。
,n∈N*。(3)若正整数n满足2≤n≤q,设k1,k2,…kn和l1,l2,…ln是1,2,…,n的两个不同的排列,c1=
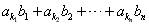 ,c2=
,c2=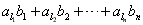 ,证明c1≠c2。
,证明c1≠c2。解:(1)由题设,可得
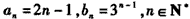
所以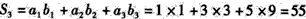 ;
;
(2)由题设,可得
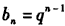
则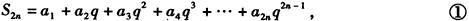
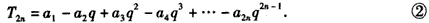
①式减去②式,得
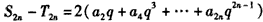
①式加上②式,得
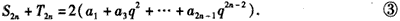
③式两边同乘q,得
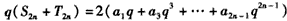
所以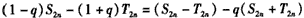
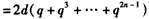
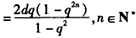 ;
;
(3)证明: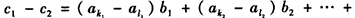
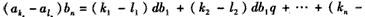
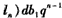
因为d≠0,b1≠0,
所以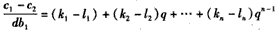
(i)若kn≠ln,取i=n
(ii)若kn=ln,取i满足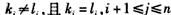
由(i),(ii)及题设知,1<i≤n,且
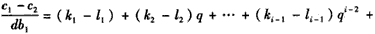
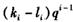
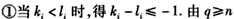

即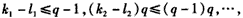
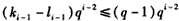
又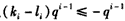
所以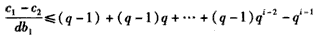
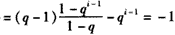
因此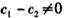
即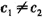 。
。
②当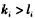 时,同理可得
时,同理可得
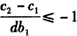
因此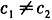
综上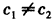 。
。
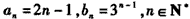
所以
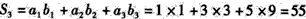 ;
;(2)由题设,可得
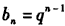
则
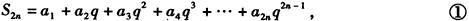
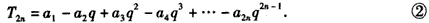
①式减去②式,得
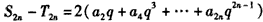
①式加上②式,得
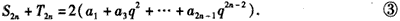
③式两边同乘q,得
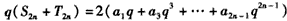
所以
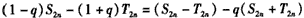
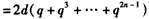
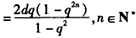 ;
;(3)证明:
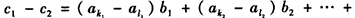
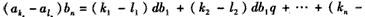
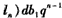
因为d≠0,b1≠0,
所以
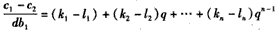
(i)若kn≠ln,取i=n
(ii)若kn=ln,取i满足
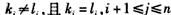
由(i),(ii)及题设知,1<i≤n,且
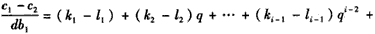
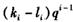
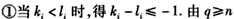

即
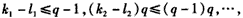
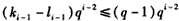
又
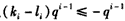
所以
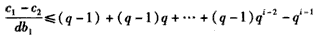
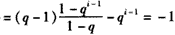
因此
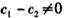
即
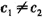 。
。②当
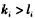 时,同理可得
时,同理可得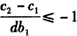
因此
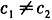
综上
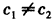 。
。
练习册系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.