��Ŀ����
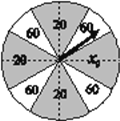
����Ŀ��ij���ͳ�����Ե��쵱�칺����![]() Ԫ�Ĺ˿ͽ��л����������涨���˿�ת��ʮ���ȷ����ʵؾ��ȵ�Բ��ת�̣���ͼ������ת��ֹͣת��ʱ����ָ��ָ������������˿Ϳ���ȡ�������Ӧ����λ��Ԫ���ij��д���ȯ������ת��ÿ��ת���Ľ������Ӱ�죮
Ԫ�Ĺ˿ͽ��л����������涨���˿�ת��ʮ���ȷ����ʵؾ��ȵ�Բ��ת�̣���ͼ������ת��ֹͣת��ʱ����ָ��ָ������������˿Ϳ���ȡ�������Ӧ����λ��Ԫ���ij��д���ȯ������ת��ÿ��ת���Ľ������Ӱ�죮
������![]() ����˿�ת��һ��ת�̻��
����˿�ת��һ��ת�̻��![]() Ԫ����ȯ�ĸ��ʣ�
Ԫ����ȯ�ĸ��ʣ�
����ij�˿Ϳ�������ת������ת�̲������Ӧ��������![]() ʱ����ù˿͵�һ�λ�ô���ȯ�������ڵڶ��λ�ô���ȯ�����ĸ��ʣ�
ʱ����ù˿͵�һ�λ�ô���ȯ�������ڵڶ��λ�ô���ȯ�����ĸ��ʣ�
�������ǹ˿�ÿ��ת��ת�̻�ô���ȯ�����Ϊ![]() ����
����![]() ȡ��ֵʱ��
ȡ��ֵʱ�� ![]() �ķ�����С��
�ķ�����С��
�����۲�Ҫ��֤����
���𰸡�(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
������������������������ü��θ��͵ĸ��ʹ�ʽ������⣻�������û����¼��ĸ��ʹ�ʽ��������¼�ͬʱ�����ĸ��ʹ�ʽ������⣻�������÷��ʽ�������.
����������������¼�![]() Ϊ���˿�ת��һ��ת�̻��
Ϊ���˿�ת��һ��ת�̻��![]() Ԫ����ȯ����
Ԫ����ȯ����
������֪![]() .
.
�������¼�![]() Ϊ���˿͵�һ�λ�ô���ȯ�����ڵڶ��λ�õĴ���ȯ�������
Ϊ���˿͵�һ�λ�ô���ȯ�����ڵڶ��λ�õĴ���ȯ�������
���¼�![]() Ϊ���ù˿͵�
Ϊ���ù˿͵�![]() ת��ת�̻�õij��д���ȯ���Ϊ
ת��ת�̻�õij��д���ȯ���Ϊ![]() ����
���� ![]() .
.
������֪�� ![]() ��
�� ![]() .
.
���![]()
![]()
![]() .
.
������![]() .
.

��ϰ��ϵ�д�
 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д� Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
�����Ŀ