题目内容
已知函数f(x)=|x|·(x﹣a).
(1)判断f(x)的奇偶性;
(2)设函数f(x)在区间[0,2]上的最小值为m(a),求m(a)的表达式;
(3)若a=4,证明:方程f(x)+ =0有两个不同的正数解.
=0有两个不同的正数解.
(1)判断f(x)的奇偶性;
(2)设函数f(x)在区间[0,2]上的最小值为m(a),求m(a)的表达式;
(3)若a=4,证明:方程f(x)+
 =0有两个不同的正数解.
=0有两个不同的正数解.解:(1)∵f(x)=|x| (x﹣a).
(x﹣a).
∴a=0时,f(x)=|x|x是奇函数;
a≠0时,f(x)=|x| (x﹣a)既不是奇函数也不是偶函数.
(x﹣a)既不是奇函数也不是偶函数.
(2)当x∈[0,2]时,f(x)=x2﹣ax=(x﹣ )2﹣
)2﹣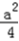 ,
,
函数f(x)图象的对称轴为直线x= .
.
当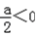 ,即a<0时,函数f(x)在[0,2]上是增函数,
,即a<0时,函数f(x)在[0,2]上是增函数,
所以m(a)=f(0)=0;
当0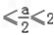 ,即0≤a≤4时,函数f(x)在[0,
,即0≤a≤4时,函数f(x)在[0, ]上是减函数,在[
]上是减函数,在[ ,2]上是增函数,
,2]上是增函数,
所以m(a)=f( )=﹣
)=﹣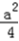 ;
;
当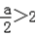 ,即a>4时,函数f(x)在[0,2]上是减函数,
,即a>4时,函数f(x)在[0,2]上是减函数,
所以m(a)=f(2)=4﹣2a.
综上,m(a)=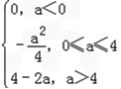 .
.
(3)证明:若a=4,则x>0时,f(x)=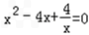 ,
,
方程可化为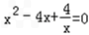 ,即
,即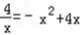 .
.
令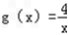 ,h(x)=﹣x2+4x,
,h(x)=﹣x2+4x,
在同一直角坐标系中作出函数g(x),h(x)在x>0时的图象.
因为g(2)=2,h(2)=4,
所以h(2)>g(2),
即当x=2时,函数h(x)图象上的点在函数g(x)图象点的上方.
所以函数g(x)与h(x)的图象在第一象限有两个不同交点.
即方程f(x)+ =0有两个不同的正数解.
=0有两个不同的正数解.
 (x﹣a).
(x﹣a). ∴a=0时,f(x)=|x|x是奇函数;
a≠0时,f(x)=|x|
 (x﹣a)既不是奇函数也不是偶函数.
(x﹣a)既不是奇函数也不是偶函数.(2)当x∈[0,2]时,f(x)=x2﹣ax=(x﹣
 )2﹣
)2﹣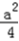 ,
,函数f(x)图象的对称轴为直线x=
 .
.当
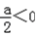 ,即a<0时,函数f(x)在[0,2]上是增函数,
,即a<0时,函数f(x)在[0,2]上是增函数,所以m(a)=f(0)=0;
当0
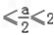 ,即0≤a≤4时,函数f(x)在[0,
,即0≤a≤4时,函数f(x)在[0, ]上是减函数,在[
]上是减函数,在[ ,2]上是增函数,
,2]上是增函数,所以m(a)=f(
 )=﹣
)=﹣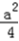 ;
;当
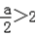 ,即a>4时,函数f(x)在[0,2]上是减函数,
,即a>4时,函数f(x)在[0,2]上是减函数,所以m(a)=f(2)=4﹣2a.
综上,m(a)=
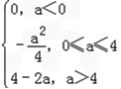 .
.(3)证明:若a=4,则x>0时,f(x)=
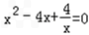 ,
,方程可化为
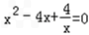 ,即
,即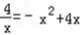 .
.令
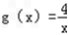 ,h(x)=﹣x2+4x,
,h(x)=﹣x2+4x,在同一直角坐标系中作出函数g(x),h(x)在x>0时的图象.
因为g(2)=2,h(2)=4,
所以h(2)>g(2),
即当x=2时,函数h(x)图象上的点在函数g(x)图象点的上方.
所以函数g(x)与h(x)的图象在第一象限有两个不同交点.
即方程f(x)+
 =0有两个不同的正数解.
=0有两个不同的正数解.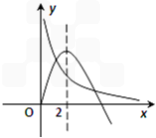

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|