题目内容
(12分)在 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
.
①求 的值;
的值;
②若 ,且
,且 ,求
,求 的值.
的值.
(Ⅰ) (Ⅱ)
(Ⅱ) 
解析试题分析:(1)第一问中根据正弦定理,化边为角,结合内角和定理,得到cosB
(2)由于利用数量积公式 ,那么根据第一问的角B的余弦值,结合余弦定理得到关于a,c的方程得到求解。
,那么根据第一问的角B的余弦值,结合余弦定理得到关于a,c的方程得到求解。
(Ⅰ)解:由正弦定理得 ,
, 因此
因此 ………6分
………6分
(Ⅱ)解:由 ,
,
所以 ………12分
………12分
考点:本试题主要是考查了解三角形中正弦定理和余弦定理的运用。
点评:解决该试题的关键是合理使用正弦定理化边为角,得到三角函数关系式,然后得到结论。也可以通过余弦定理化角为边,得到三边的平方关系式,得到角B的余弦值。

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 ,已知S的身高约为
,已知S的身高约为 米(将眼睛距地面的距离按
米(将眼睛距地面的距离按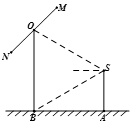
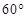 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由. 中,内角
中,内角 所对边的长分别为
所对边的长分别为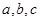 ,已知向量
,已知向量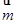 ="(1,cosA" -1),
="(1,cosA" -1),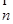 =(cosA,1)且满足
=(cosA,1)且满足 的大小;
的大小; ,求
,求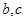 的值.
的值.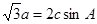
 ,且△ABC的面积为
,且△ABC的面积为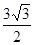
 ,求a+b的值。
,求a+b的值。 、
、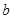 、
、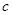 分别是
分别是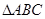 的三个内角
的三个内角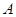 、
、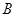 、
、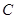 所对的边,(1)若
所对的边,(1)若 求
求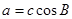 ,且
,且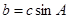 ,试判断
,试判断 ,bc=48,b-c=2,求a.
,bc=48,b-c=2,求a.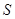 为△ABC的面积,满足
为△ABC的面积,满足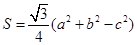 .(1)求角C的大小;(2)求
.(1)求角C的大小;(2)求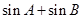 的最大值.
的最大值.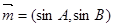 ,
,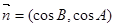 ,
,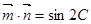 ,且
,且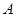 、
、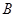 、
、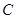 分别为
分别为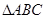 的三边
的三边 、
、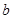 、
、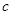 所对的角。
所对的角。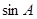 ,
,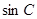 ,
,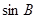 成等差数列,且
成等差数列,且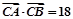 ,求
,求 中,角
中,角 为锐角,记角
为锐角,记角 所对的边分别为
所对的边分别为 ,设向量
,设向量 ,且
,且 的夹角为
的夹角为
 的值及角
的值及角 ,求
,求 .
.