题目内容
已知函数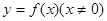 对于任意的
对于任意的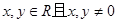 满足
满足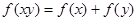 .
.
(1)求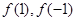 的值;
的值;
(2)求证: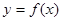 为偶函数;
为偶函数;
(3)若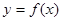 在
在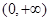 上是增函数,解不等式
上是增函数,解不等式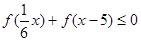
【答案】
(1)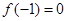 。
。
(2)令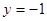 ,得
,得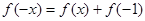 ,可得
,可得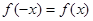 。
。
(3)不等式的解集为:[-1,0)∪(0,2]∪[3,5)∪(5,6]。
【解析】
试题分析:(1)解:∵对于任意的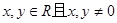 满足
满足
∴令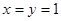 ,得到:
,得到: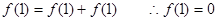
令 ,得到:
,得到: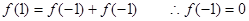 4分
4分
(2)证明:有题可知,令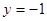 ,得
,得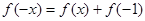
∵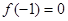 ∴
∴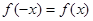 ∴
∴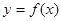 为偶函数; 8分
为偶函数; 8分
(3)由(2) 函数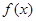 是定义在非零实数集上的偶函数.
是定义在非零实数集上的偶函数.
∴不等式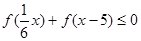 可化为
可化为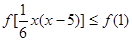
∴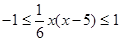 .即:
.即: 且
且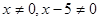
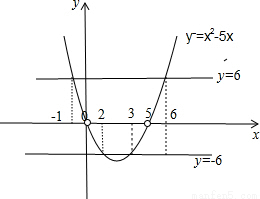
在坐标系内,如图函数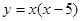 图象与
图象与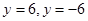 两直线.
两直线.
由图可得x∈[-1,0)∪(0,2]∪[3,5)∪(5,6]
故不等式的解集为:[-1,0)∪(0,2]∪[3,5)∪(5,6] 12分
考点:抽象函数,函数的奇偶性,函数的图象,抽象不等式。
点评:中档题,抽象函数问题,往往利用“赋值法”。抽象不等式问题,往往要利用函数的单调性,结合函数的图象分析得解。

练习册系列答案
相关题目
 ,若存在x0∈R,使
,若存在x0∈R,使 成立,则称x0为
成立,则称x0为 (a≠0)。
(a≠0)。 时,求函数
时,求函数 图象上A、B两点的横坐标是函数
图象上A、B两点的横坐标是函数 对称,求
对称,求 的的最小值。
的的最小值。