题目内容
已知函数f(x)=ex+2x2-ax.(Ⅰ)函数f(x)在区间[0,1]上存在唯一的极值点,求a的取值范围.
(Ⅱ)若a=3,当
 时,关于x的不等式
时,关于x的不等式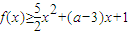 恒成立,试求实数a的取值范围.
恒成立,试求实数a的取值范围.
【答案】分析:(I)由已知中函数的解析式,我求出函数的导函数的解析式,然后根据函数f(x)在区间[0,1]上存在唯一的极值点,即导函数在区间[0,1]上存在唯一的零点,即f'(0)•f'(1)<0,解不等式即可得到满足条件的a的取值范围.
(Ⅱ)将a=3代入,并构造函数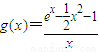 ,利用导数法求出函数的最小值,然后根据函数恒成立的性质,即可求出满足条件的实数a的取值范围.
,利用导数法求出函数的最小值,然后根据函数恒成立的性质,即可求出满足条件的实数a的取值范围.
解答:解:(Ⅰ)f′(x)=ex+4x-a,
∵f′(0)=1-a,f′(1)=e+4-a,
又∵函数f(x)在区间[0,1]上存在唯一的极值点
∴f'(0)•f'(1)<0.
∴1<a<e+4
(Ⅱ)由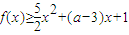 ,得
,得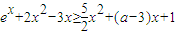 ,
,
即 ,
,
∵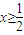 ,∴
,∴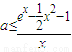 ,
,
令 ,则
,则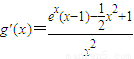 .
.
令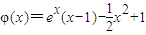 ,则φ'(x)=x(ex-1).
,则φ'(x)=x(ex-1).
∵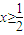 ,∴φ'(x)>0,∴φ(x)在
,∴φ'(x)>0,∴φ(x)在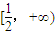 上单调递增,
上单调递增,
∴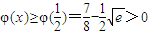 ,
,
因此g'(x)>0,故g(x)在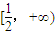 上单调递增,
上单调递增,
则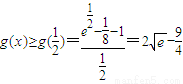 ,∴a的取值范围是
,∴a的取值范围是 .
.
点评:本题考查的知识点是函数在某点取得极值的条件及导数在最大值、最小值问题中的应用,其中根据已知中函数的解析式,求出函数的导函数的解析式是解答此类问题的关键.
(Ⅱ)将a=3代入,并构造函数
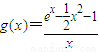 ,利用导数法求出函数的最小值,然后根据函数恒成立的性质,即可求出满足条件的实数a的取值范围.
,利用导数法求出函数的最小值,然后根据函数恒成立的性质,即可求出满足条件的实数a的取值范围.解答:解:(Ⅰ)f′(x)=ex+4x-a,
∵f′(0)=1-a,f′(1)=e+4-a,
又∵函数f(x)在区间[0,1]上存在唯一的极值点
∴f'(0)•f'(1)<0.
∴1<a<e+4
(Ⅱ)由
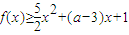 ,得
,得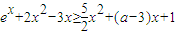 ,
,即
 ,
,∵
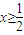 ,∴
,∴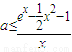 ,
,令
 ,则
,则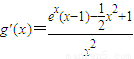 .
.令
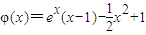 ,则φ'(x)=x(ex-1).
,则φ'(x)=x(ex-1).∵
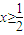 ,∴φ'(x)>0,∴φ(x)在
,∴φ'(x)>0,∴φ(x)在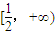 上单调递增,
上单调递增,∴
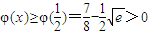 ,
,因此g'(x)>0,故g(x)在
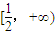 上单调递增,
上单调递增,则
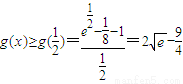 ,∴a的取值范围是
,∴a的取值范围是 .
.点评:本题考查的知识点是函数在某点取得极值的条件及导数在最大值、最小值问题中的应用,其中根据已知中函数的解析式,求出函数的导函数的解析式是解答此类问题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目