题目内容
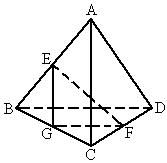
 如图,正三棱锥A-BCD的底面边长为2,侧棱长为3,E为棱BC的中点.
如图,正三棱锥A-BCD的底面边长为2,侧棱长为3,E为棱BC的中点.(1)求该三棱锥的表面积S;
(2)求异面直线AE与CD所成角的大小(结果用反三角函数值表示).
分析:(1)由题意可得斜高AE,可得三角形的侧面面积,加上底面可得;
(2)取BD中点F,连结AF、EF,可得∠AEF就是异面直线AE与CD所成的角(或其补角),在△AEF中可得cos∠AEF,由反三角函数可得.
(2)取BD中点F,连结AF、EF,可得∠AEF就是异面直线AE与CD所成的角(或其补角),在△AEF中可得cos∠AEF,由反三角函数可得.
解答:解:(1)由题意结合勾股定理可得:
正三棱锥的斜高AE=
=
=2
∴表面积S=
×22+3×
×2×2
=
+6
(2)取BD中点F,连结AF、EF,
∵EF∥CD,∴∠AEF就是异面直线AE与CD所成的角(或其补角),
在△AEF中,AE=AF=2
,EF=1,
∴cos∠AEF=
=
.
∴异面直线AE与CD所成的角的大小为arccos
.
正三棱锥的斜高AE=
| AB2-BE2 |
| 32-12 |
| 2 |
∴表面积S=
| ||
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
(2)取BD中点F,连结AF、EF,
∵EF∥CD,∴∠AEF就是异面直线AE与CD所成的角(或其补角),
在△AEF中,AE=AF=2
| 2 |
∴cos∠AEF=
| ||
2
|
| ||
| 8 |
∴异面直线AE与CD所成的角的大小为arccos
| ||
| 8 |
点评:本题考查异面直线所成的角,涉及反三角函数和表面积的求解,属中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
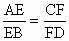 ,设a
为EF与AC所成角,b
为EF与BD所成的角,则a
+b
等于
,设a
为EF与AC所成角,b
为EF与BD所成的角,则a
+b
等于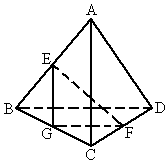
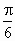
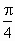
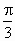
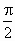
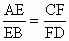 ,设a
为EF与AC所成角,b
为EF与BD所成的角,则a
+b
等于
,设a
为EF与AC所成角,b
为EF与BD所成的角,则a
+b
等于
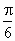
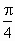
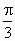
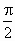


 (0<λ<+∞),设α为异面直线EF与AC所成的角,β为异面直线EF与BD所成的角,则α+β的值是( )
(0<λ<+∞),设α为异面直线EF与AC所成的角,β为异面直线EF与BD所成的角,则α+β的值是( )


