Question

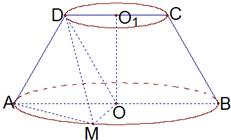（2010•台州二模）如图，四边形ABCD是圆台OO₁的轴截面，AB=2CD=4，点M在底面圆周上，且∠AOM=

π

2

，DM⊥AC．
（I）求圆台OO₁的体积；
（II）求二面角A-DM-O的余弦值．

Answer 1

分析：（I）由已知中∠AOM=

π

2

，可得OO₁、OM、OB两两互相垂直，故可以O为原点，分别以直线OM、OB、OO₁为x、y、z轴建立空间直角坐标系，求出圆台的高OO₁=h值后，代入圆台OO₁的体积公式V=

1

3

πh(r12+r1r2+

r

2 2

)即可得到答案．
（II）分别求出平面ADM、平面ODM的法向量，代入向量夹角公式，即可得到二面角A-DM-O的余弦值．

解答：解：（I）由题意可得OO₁、OM、OB两两互相垂直，
以O为原点，分别以直线OM、OB、OO₁为x、y、z轴建立空间直角坐标系-----（2分）
设OO₁=h（h＞0），则D（0，-1，h），M（2，0，0），A（0，-2，0），C（0，1，h）∴

DM

=(2，1，-h)，

AC

=(0，3，h)w∵DM⊥AC∴

DM

•

AC

=3-h2=0
解得h=

3

------（6分）∴圆台OO₁的体积V=

1

3

πh(r12+r1r2+

r

2 2

)=

7 3 π

3

．------（7分）
（II）

AM

=(2，2，0)，

DM

=(2，1，-

3

)，

OM

=(2，0，0)
设平面ADM、平面ODM的法向量分别为

u

=(x1，y1，z1)，

v

=(x2，y2，z2)
则

u • AM =0                 u • DM =0

且 

v • DM =0                 v • OM =0

即

2x1+2y1=0 2x1+y1- 3 z1=0

且 

2x2+y2- 3 z2=0 2x2=0

取

u

=(1，-1，

3

3

)

v

=(0，3，

3

)------（11分）∴cos＜

u

，

v

＞=

u • v

| u |•| v |

=-

7

7

．------（13分）
则二面角A-DM-O的余弦值为

7

7

------（14分）

点评：本题考查的知识点是用空间向量求平面间的夹角，圆台的体积，其中（I）的关键是求出圆台的高，熟练掌握圆台的体积公式，（II）的关键是求出两个平面的法向量．