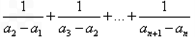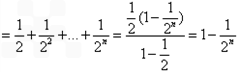题目内容
已知数列 满足:
满足:
 ,且数列
,且数列 为等差数列.
为等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)求和: .
.
 满足:
满足:
 ,且数列
,且数列 为等差数列.
为等差数列. (1)求数列
 的通项公式;
的通项公式;(2)求和:
 .
.解:(1)等差数列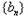 的首项为
的首项为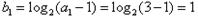 ,
,
公差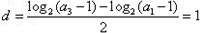
∴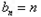
即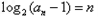
∴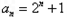 .
.
(2)∵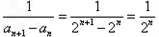 .
.
∴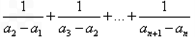
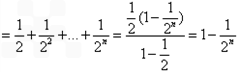
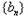 的首项为
的首项为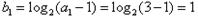 ,
,公差
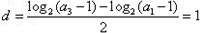
∴
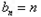
即
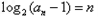
∴
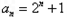 .
. (2)∵
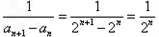 .
.∴
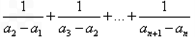
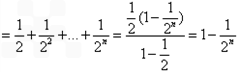

练习册系列答案
相关题目
题目内容
 满足:
满足:
 ,且数列
,且数列 为等差数列.
为等差数列.  的通项公式;
的通项公式; .
.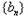 的首项为
的首项为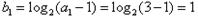 ,
,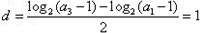
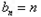
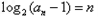
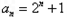 .
. 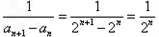 .
.