Question

ABCD与CDEF是两个全等的正方形，且两个正方形所在平面互相垂直，则DF与AC所成角的大小为

 

．

Answer 1

分析：作出如图的图形，取H，M，N为三个线线段的中点，可以证得∠HMN即为DF与AC所成角可所成角的补角，在三角形HMN中求解即可

解答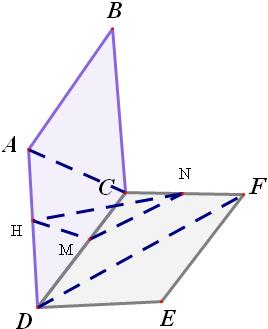：解：如图不妨令正方形的边长为2，则AC=DF=2

2

，取H，M，N为三个线线段的中点，连接HM，MN，则有HM∥AC，MN∥DF，故∠HMN即为DF与AC所成角可所成角且HM=MN=

2

连接HN，DN，在直角三角形DCN中可以求得ND=

5

，
在直角三角形HDN中可以求得HN=

6

在△HMN中cos∠HMN=

2+2-6

2× 2 × 2

=-

1

2

故∠HMN=

2π

3

所以DF与AC所成角的大小为

π

3

故答案为

π

3

点评：本题考查异面直线所成角的求法，其步骤是作角，证角，求角，在解三角形求所成角的余弦时，如本题中，解得余弦值为负，对应的角是一个钝角，则两直线所成的角是它的补角，若求出的余弦值是正值，则所求的角即为两异面直线所成的角．