题目内容
16.某商品的进价是40元/kg,现在的售价是60元/kg,每周可卖出300kg.根据市场调查,该商品每涨价1元,每周要少卖出10kg;每降价1元,每周可多卖出20kg.如果要对该商品涨价,那么涨价的范围是多少才能使每周的利润不少于6240元?如果要对该商品降价,那么降价的范围是多少才能使每周的利润不少于6240元?分析 设价格浮动为x元,根据已知构造相应不等式,解得答案.
解答 解:设涨价x元才能使每周的利润不少于6240元,
则(60+x-40)(300-10x)≥6240,x>0,
解得:4≤x≤6,
故涨价的范围在[4,6]时才能使每周的利润不少于6240元;
设降价x元才能使每周的利润不少于6240元,
则(60-x-40)(300+20x)≥6240,x>0,
此时不等式无解,
故只要降价就会使每周的利润少于6240元;
点评 本题考查的知识点是不等式的应用,根据已知构造满足条件的不等式,是解答的关键.

练习册系列答案
相关题目
6.设函数f(x)=-$\frac{5}{3}$x3+bx-c,其导数为f′(x),若f′(1)=-2,则二项式(bx+$\frac{1}{x}$)5的展开式中x3的系数为( )
| A. | 10250 | B. | 3430 | C. | 825 | D. | 405 |
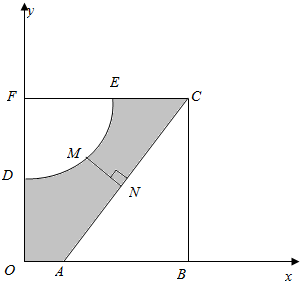 如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF=$\frac{9}{4}$km,FE=3km,EC=$\frac{3}{2}$km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=$\frac{x+b}{x+a}$(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分.
如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF=$\frac{9}{4}$km,FE=3km,EC=$\frac{3}{2}$km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=$\frac{x+b}{x+a}$(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分.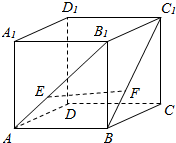 如图,正方体ABCD-A1B1C1D1,E,F分别在AB1,BC1上,且$\frac{{B}_{1}E}{AE}$=$\frac{{C}_{1}F}{BF}$=2,过EF做一个平面和面ABCD相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)
如图,正方体ABCD-A1B1C1D1,E,F分别在AB1,BC1上,且$\frac{{B}_{1}E}{AE}$=$\frac{{C}_{1}F}{BF}$=2,过EF做一个平面和面ABCD相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线) 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率为$\frac{1}{2}$.过原点的直线与椭圆C交于A、B两点(A,B不是椭圆C的顶点),点D在椭圆C上,且AD⊥AB.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率为$\frac{1}{2}$.过原点的直线与椭圆C交于A、B两点(A,B不是椭圆C的顶点),点D在椭圆C上,且AD⊥AB. 围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需要维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米),修建此矩形场地围墙的总费用为y(单位:元).
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需要维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米),修建此矩形场地围墙的总费用为y(单位:元).