题目内容
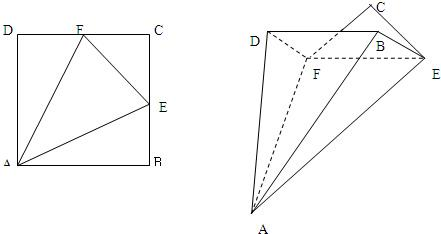
（2010•合肥模拟）已知四边形ABCD是边长为2
的正方形，E，F分别为BC，CD的中点，沿AE，AF，EF将△ABE，△ADF，△CEF向同侧折叠且与平面y1+y2=
成直二面角，连接BD．
（1）求证BD⊥AC；
（2）求面AEF 与面ABE所成锐角的余弦值．
| 2 |
| 16t |
| t2+32 |
（1）求证BD⊥AC；
（2）求面AEF 与面ABE所成锐角的余弦值．
分析：方法一（1）以EF的中点O为原点，OA为x轴，OE为y轴，OC为z轴建立直角坐标系，写出要用的点的坐标，在两条直线上取方向向量，根据两个向量的数量积得到两条直线之间的关系．
（2）设出两个平面的法向量，根据法向量与平面上的向量垂直，做出两个数量积等于0的式子，求出一个法向量，根据两个向量的夹角的余弦的绝对值等于所求的结果．
方法二：（1）做出辅助线过D作DH⊥AF于H，过B作BG⊥AE于G，根据两个三角形全等得到线段之间的关系，得到线面垂直，根据线面垂直得到线与线垂直．
（2）根据面ABE⊥面AEF，面CEF⊥面AEF，得到面ABE与面CEF的交线必与面AEF垂直，故∠AEF为二面角平面角，再把二面角放到一个可解的三角形中求出角的余弦值．
（2）设出两个平面的法向量，根据法向量与平面上的向量垂直，做出两个数量积等于0的式子，求出一个法向量，根据两个向量的夹角的余弦的绝对值等于所求的结果．
方法二：（1）做出辅助线过D作DH⊥AF于H，过B作BG⊥AE于G，根据两个三角形全等得到线段之间的关系，得到线面垂直，根据线面垂直得到线与线垂直．
（2）根据面ABE⊥面AEF，面CEF⊥面AEF，得到面ABE与面CEF的交线必与面AEF垂直，故∠AEF为二面角平面角，再把二面角放到一个可解的三角形中求出角的余弦值．
解答：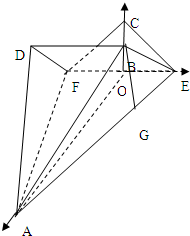
解：（1）方法一：以EF的中点O为原点，OA为x轴，OE为y轴，OC为z轴建立直角坐标系，则C（0，0，1），A（3，0，0），E（0，1，0），解正方形可得B(
，
，
)，D(
，-
，
)∴
=（-3，0，1），
=(0，-
，0)
∵
•
=0，∴
⊥
∴BD⊥AC
（2）∵OA⊥面CEF，∴面CEF的法向量为
=（3，0，0）
设面ABE的法向量为
=（x，y，z）∵
，
得
⇒
令x=1，得一个法向量为
=(1，3，0)，设锐二面角为θ
则cosθ=|
|=|
|=
方法二（1）过D作DH⊥AF于H，过B作BG⊥AE于G．
∵△ABE≌△ADF，∴BG=DH
又面ABG⊥面AEF，∴DH⊥面AEF，∴BG∥DH
故四边形BDHG为平行四边形，∴BD∥GH
取EF中点为O，连CO、AO
则CO⊥EF，AO⊥EF，∴EF⊥面ACO
又GH∥EF，∴BD∥EF，∴BD⊥面ACO，∴BD⊥AC
（2）∵面ABE⊥面AEF，面CEF⊥面AEF
∴面ABE与面CEF的交线必与面AEF垂直，
故∠AEF为二面角平面角．
在△AEF中，AE=
，EF=2，
∴cos∠AEF=
=
=
故二面角的余弦值为
．
解：（1）方法一：以EF的中点O为原点，OA为x轴，OE为y轴，OC为z轴建立直角坐标系，则C（0，0，1），A（3，0，0），E（0，1，0），解正方形可得B(| 3 |
| 5 |
| 4 |
| 5 |
2
| ||
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
2
| ||
| 5 |
| AC |
| BD |
| 8 |
| 5 |
∵
| AC |
| BD |
| AC |
| BD |
∴BD⊥AC
（2）∵OA⊥面CEF，∴面CEF的法向量为
| OA |
设面ABE的法向量为
| n |
|
得
|
|
令x=1，得一个法向量为
| n |
则cosθ=|
| ||||
|
|
| 3 | ||
3•
|
| ||
| 10 |
方法二（1）过D作DH⊥AF于H，过B作BG⊥AE于G．
∵△ABE≌△ADF，∴BG=DH
又面ABG⊥面AEF，∴DH⊥面AEF，∴BG∥DH
故四边形BDHG为平行四边形，∴BD∥GH
取EF中点为O，连CO、AO
则CO⊥EF，AO⊥EF，∴EF⊥面ACO
又GH∥EF，∴BD∥EF，∴BD⊥面ACO，∴BD⊥AC
（2）∵面ABE⊥面AEF，面CEF⊥面AEF
∴面ABE与面CEF的交线必与面AEF垂直，
故∠AEF为二面角平面角．
在△AEF中，AE=
| 10 |
∴cos∠AEF=
| ||
| AE |
| 1 | ||
|
| ||
| 10 |
故二面角的余弦值为
| ||
| 10 |
点评：本题考查线与线垂直和面与面的夹角，本题可以采用建立坐标系，把几何证明转化为向量之间的运算，也可以利用严格的推理过程利用几何方法来解题．
练习册系列答案
走进文言文系列答案
相关题目
