题目内容
已知x∈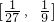
，函数f（x）=log3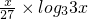
（1）求函数f（x）最大值和最小值；
（2）若方程f（x）+m=0有两根α，β，试求αβ的值
解：（1）f（x）=（log3x-3）（log3x+1）=（log3x）2-2log3x-3
令log3x=t，由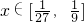
得，t∈[-3，-2]
∴y=t2-2t-3，t∈[-3，-2]
当t=-3时，ymax=12
当t=-2时，ymin=5
（2）（log3x）2-2log3x-3+m=0，有两个根α、β
令log3x=t，则t2-2t-3+m=0也有两根，不妨设t1=log3α，t2=log3β
则t1+t2=log3α+log3β=log3（αβ）=2
∴αβ=9
分析：（1）将函数变形f（x）=（log3x-3）（log3x+1）=（log3x）2-2log3x-3，令log3x=t，转化为二次函数解决．
（2）方程f（x）+m=0有两根α，β，令log3x=t，则t2-2t-3+m=0也有两根，再用韦达定理求解．
点评：本题主要考查一般函数通过变形转化为基本函数解决问题的能力．
令log3x=t，由
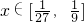得，t∈[-3，-2]∴y=t2-2t-3，t∈[-3，-2]
当t=-3时，ymax=12
当t=-2时，ymin=5
（2）（log3x）2-2log3x-3+m=0，有两个根α、β
令log3x=t，则t2-2t-3+m=0也有两根，不妨设t1=log3α，t2=log3β
则t1+t2=log3α+log3β=log3（αβ）=2
∴αβ=9
分析：（1）将函数变形f（x）=（log3x-3）（log3x+1）=（log3x）2-2log3x-3，令log3x=t，转化为二次函数解决．
（2）方程f（x）+m=0有两根α，β，令log3x=t，则t2-2t-3+m=0也有两根，再用韦达定理求解．
点评：本题主要考查一般函数通过变形转化为基本函数解决问题的能力．
练习册系列答案
优等生题库系列答案
相关题目
已知函数f（x）、g（x），下列说法正确的是（ ）
| A、f（x）是奇函数，g（x）是奇函数，则f（x）+g（x）是奇函数 | B、f（x）是偶函数，g（x）是偶函数，则f（x）+g（x）是偶函数 | C、f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）一定是奇函数或偶函数 | D、f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）可以是奇函数或偶函数 |