题目内容
动点M的坐标(x,y)在其运动过程中总满足关系式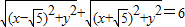 .
.(1)点M的轨迹是什么曲线?请写出它的标准方程;
(2)已知定点T(t,0)(0<t<3),若|MT|的最小值为1,求t的值;
(3)设直线l不经过原点O,与动点M的轨迹相交于A,B两点,点G为线段AB的中点,直线OG与该轨迹相交于C,D两点,若直线AB,CD,AC,AD,DB,BC的斜率分别为k1,k2,k3,k4,k5,k6,求证:k1•k2=k3•k4=k5•k6.
【答案】分析:(1)根据 ,可得(x,y)到
,可得(x,y)到 ,
, 的距离的和为6,大于两定点间的距离
的距离的和为6,大于两定点间的距离 ,故点M的轨迹是焦点在x轴上的椭圆,且a=3,c=
,故点M的轨迹是焦点在x轴上的椭圆,且a=3,c= ,从而可求椭圆的标准方程;
,从而可求椭圆的标准方程;
(2) ,0≤x≤3,构造函数,配方可得
,0≤x≤3,构造函数,配方可得 ,0≤x≤3,再进行分类讨论,利用|MT|的最小值为1,即可求t的值;
,0≤x≤3,再进行分类讨论,利用|MT|的最小值为1,即可求t的值;
(3)设A(x1,y1),B(x2,y2),G(x,y),则x1+x2=2x,y1+y2=2y,设C(x3,y3),则D(-x3,-y3)
根据点在椭圆上,利用点差法,即可证得结论.
解答:(1)解:∵ .
.
∴(x,y)到 ,
, 的距离的和为6,大于两定点间的距离
的距离的和为6,大于两定点间的距离
∴点M的轨迹是焦点在x轴上的椭圆,且a=3,c=
∴b2=4
∴椭圆的标准方程为:
(2)解: ,0≤x≤3
,0≤x≤3
记 ,0≤x≤3
,0≤x≤3
①当 ,即
,即 时,
时, ,
,
又 ,∴
,∴ ,解得
,解得 ,而
,而 ,故舍去
,故舍去
②当 ,即
,即 时,
时, ,
,
又 ,∴t2-6t+9=1,解得t=2或t=4,而
,∴t2-6t+9=1,解得t=2或t=4,而 ,故舍去
,故舍去
又 ,故t=2符合题意;综上可知,t=2
,故t=2符合题意;综上可知,t=2
(3)证明:设A(x1,y1),B(x2,y2),G(x,y),则x1+x2=2x,y1+y2=2y
由
∴ ,
,
设C(x3,y3),则D(-x3,-y3)
由 ,
,
∴ ,
,
同理 ,
,
∴k1•k2=k3•k4=k5•k6
点评:本题考查椭圆的定义,考查椭圆的标准方程,考查分类讨论的数学思想,考查配方法求函数的最值,考查点差法的运用,解题的关键是正确分类,合理运用点差法.
 ,可得(x,y)到
,可得(x,y)到 ,
, 的距离的和为6,大于两定点间的距离
的距离的和为6,大于两定点间的距离 ,故点M的轨迹是焦点在x轴上的椭圆,且a=3,c=
,故点M的轨迹是焦点在x轴上的椭圆,且a=3,c= ,从而可求椭圆的标准方程;
,从而可求椭圆的标准方程;(2)
 ,0≤x≤3,构造函数,配方可得
,0≤x≤3,构造函数,配方可得 ,0≤x≤3,再进行分类讨论,利用|MT|的最小值为1,即可求t的值;
,0≤x≤3,再进行分类讨论,利用|MT|的最小值为1,即可求t的值;(3)设A(x1,y1),B(x2,y2),G(x,y),则x1+x2=2x,y1+y2=2y,设C(x3,y3),则D(-x3,-y3)
根据点在椭圆上,利用点差法,即可证得结论.
解答:(1)解:∵
 .
.∴(x,y)到
 ,
, 的距离的和为6,大于两定点间的距离
的距离的和为6,大于两定点间的距离
∴点M的轨迹是焦点在x轴上的椭圆,且a=3,c=

∴b2=4
∴椭圆的标准方程为:

(2)解:
 ,0≤x≤3
,0≤x≤3记
 ,0≤x≤3
,0≤x≤3①当
 ,即
,即 时,
时, ,
,又
 ,∴
,∴ ,解得
,解得 ,而
,而 ,故舍去
,故舍去②当
 ,即
,即 时,
时, ,
,又
 ,∴t2-6t+9=1,解得t=2或t=4,而
,∴t2-6t+9=1,解得t=2或t=4,而 ,故舍去
,故舍去又
 ,故t=2符合题意;综上可知,t=2
,故t=2符合题意;综上可知,t=2(3)证明:设A(x1,y1),B(x2,y2),G(x,y),则x1+x2=2x,y1+y2=2y
由

∴
 ,
,设C(x3,y3),则D(-x3,-y3)
由
 ,
,∴
 ,
,同理
 ,
,∴k1•k2=k3•k4=k5•k6
点评:本题考查椭圆的定义,考查椭圆的标准方程,考查分类讨论的数学思想,考查配方法求函数的最值,考查点差法的运用,解题的关键是正确分类,合理运用点差法.

练习册系列答案
相关题目
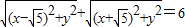 .
.