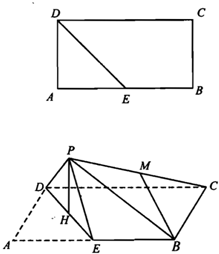
题目内容
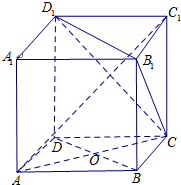
如图所示，在正方体ABCD-A1B1C1D1中E、F分别在A1D、AC上，且A1E=
A1D，AF=
AC，则（ ）
| 2 |
| 3 |
| 1 |
| 3 |
| A．EF至多与A1D、AC之一垂直 |
| B．EF是A1D、AC的公垂线 |
| C．EF与BD1相交 |
| D．EF与BD1异面 |
如图所示
设AC∩BD=O，AD1∩A1D=O1，作EG⊥AD于G，FK⊥AD于K，由平几知识，GF∥DO，DO⊥AC，∴GF⊥AC，
∵EG⊥面ABCD，∴由三垂线逆定理EF⊥AC．
同理EF⊥A1D，
∴EF是A1D、AC公垂线
故选B．
设AC∩BD=O，AD1∩A1D=O1，作EG⊥AD于G，FK⊥AD于K，由平几知识，GF∥DO，DO⊥AC，∴GF⊥AC，
∵EG⊥面ABCD，∴由三垂线逆定理EF⊥AC．
同理EF⊥A1D，
∴EF是A1D、AC公垂线
故选B．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
