题目内容
解关于x的不等式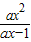 >x(a∈R).
>x(a∈R).
【答案】分析:法一是先把不等式化简以及同解变形,然后讨论变量a,解答即可.
法二是先把不等式化简以及同解变形,类似法一,在x 范围中讨论a的取值情况.
解答:解法一:由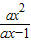 >x,得
>x,得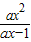 -x>0,即
-x>0,即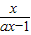 >0.
>0.
此不等式与x(ax-1)>0同解.
若a<0,则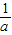 <x<0;
<x<0;
若a=0,则x<0;
若a>0,则x<0或x>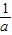 .
.
综上,a<0时,原不等式的解集是(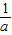 ,0);
,0);
a=0时,原不等式的解集是(-∞,0);
a>0时,原不等式的解集是(-∞,0)∪(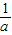 ,+∞).
,+∞).
解法二:由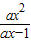 >x,得
>x,得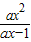 -x>0,即
-x>0,即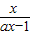 >0.
>0.
此不等式与x(ax-1)>0同解.
显然,x≠0.
(1)当x>0时,得ax-1>0.
若a<0,则x<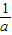 ,与x>0矛盾,
,与x>0矛盾,
∴此时不等式无解;
若a=0,则-1>0,此时不等式无解;
若a>0,则x>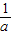 .
.
(2)当x<0时,得ax-1<0.
若a<0,则x>,得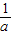 <x<0;
<x<0;
若a=0,则-1<0,得x<0;
若a>0,则x<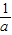 ,得x<0.
,得x<0.
综上,a<0时,原不等式的解集是(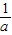 ,0);
,0);
a=0时,原不等式的解集是(-∞,0);
a>0时,原不等式的解集是(-∞,0)∪(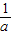 ,+∞).
,+∞).
点评:本题考查含参变数的分式不等式的解法,考查等价转化思想,是难度较大题目.
法二是先把不等式化简以及同解变形,类似法一,在x 范围中讨论a的取值情况.
解答:解法一:由
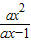 >x,得
>x,得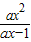 -x>0,即
-x>0,即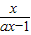 >0.
>0.此不等式与x(ax-1)>0同解.
若a<0,则
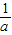 <x<0;
<x<0;若a=0,则x<0;
若a>0,则x<0或x>
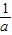 .
.综上,a<0时,原不等式的解集是(
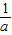 ,0);
,0);a=0时,原不等式的解集是(-∞,0);
a>0时,原不等式的解集是(-∞,0)∪(
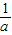 ,+∞).
,+∞).解法二:由
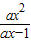 >x,得
>x,得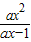 -x>0,即
-x>0,即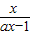 >0.
>0.此不等式与x(ax-1)>0同解.
显然,x≠0.
(1)当x>0时,得ax-1>0.
若a<0,则x<
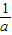 ,与x>0矛盾,
,与x>0矛盾,∴此时不等式无解;
若a=0,则-1>0,此时不等式无解;
若a>0,则x>
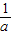 .
.(2)当x<0时,得ax-1<0.
若a<0,则x>,得
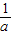 <x<0;
<x<0;若a=0,则-1<0,得x<0;
若a>0,则x<
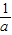 ,得x<0.
,得x<0.综上,a<0时,原不等式的解集是(
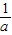 ,0);
,0);a=0时,原不等式的解集是(-∞,0);
a>0时,原不等式的解集是(-∞,0)∪(
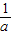 ,+∞).
,+∞).点评:本题考查含参变数的分式不等式的解法,考查等价转化思想,是难度较大题目.

练习册系列答案
相关题目