题目内容
函数 的单调递增区间是
的单调递增区间是
A. | B. | C.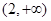 | D. |
A
解析试题分析:由 得函数的定义域为
得函数的定义域为 ,再根据复合函数的单调性可知内函数的减区间即为原函数的增区间,所以f(x)的单调递增区间为
,再根据复合函数的单调性可知内函数的减区间即为原函数的增区间,所以f(x)的单调递增区间为 .
.
考点:复合函数的定义域,单调区间。
点评:复合函数单调性的判断方法可以同则增,异则减的原则来判断。同是指内外函数的单调性相同,异是指内外函数的单调性相反。在求单调区间时要注意在定义域内进行。

练习册系列答案
相关题目
若函数 的定义域为[0 , m],值域为
的定义域为[0 , m],值域为 ,则m的取值范围是( )
,则m的取值范围是( )
| A.(0 , 4] | B.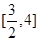 | C. | D. ) ) |
若方程 在(0,1)内恰有一解,则
在(0,1)内恰有一解,则 的取值范围是
的取值范围是
A. | B. | C. | D. |
下列各式中成立的是( )
A. | B. |
C. | D. |
若点 在函数
在函数 的图象上,则
的图象上,则 的值为( )
的值为( )
A. | B. | C. | D.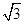 |
已知函数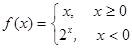 ,则
,则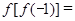 ( )
( )
A. | B.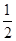 | C.1 | D.2 |
设函数 ,则
,则 =( )
=( )
| A.2 | B.6 | C.8 | D.4 |
设函数f(x) 则使得f(x)≥1的自变量x的取值范围为
则使得f(x)≥1的自变量x的取值范围为
| A.(-∞,-2]∪[0,10] | B.(-∞,-2]∪[0,1] |
| C.(-∞,-2]∪[1,10] | D.[-2,0]∪[1,10] |
二次函数y=ax2+bx+c的图象如图所示,则点(a,c) ……( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |