题目内容
 如图所示的“双塔”形立体建筑,已知P-ABD和Q-CBD是两个高相等的正三棱锥,四点A,B,C,D在同一平面内,要使塔尖P,Q之间的距离为50m,则底边AB的长为
如图所示的“双塔”形立体建筑,已知P-ABD和Q-CBD是两个高相等的正三棱锥,四点A,B,C,D在同一平面内,要使塔尖P,Q之间的距离为50m,则底边AB的长为50
| 3 |
50
m.| 3 |
分析:根据正三棱锥的性质有底面是正三角形且顶点在底面上的射影是底面正三角形的中心.设P,S在底面的射影分别为N,M,有M,N分别是正三角形BCD和正三角形ABD的中心,且PS=MN,再利用正三角形的性质得出MN的长即可求出AB.
解答: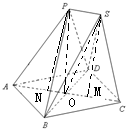 解:根据题意知,底面是正三角形且顶点在底面上的射影是底面正三角形的中心,
解:根据题意知,底面是正三角形且顶点在底面上的射影是底面正三角形的中心,
如图.
设P,S在底面的射影分别为N,M.
则M,N分别是正三角形BCD,和正三角形ABD的中心
且PS=MN,
又ON=OM=
OA=
×
AB,
∴MN=
AB,
即
AB=50,
∴AB=50
m
∴底边AB的长为 50
m
故答案为:50
 解:根据题意知,底面是正三角形且顶点在底面上的射影是底面正三角形的中心,
解:根据题意知,底面是正三角形且顶点在底面上的射影是底面正三角形的中心,如图.
设P,S在底面的射影分别为N,M.
则M,N分别是正三角形BCD,和正三角形ABD的中心
且PS=MN,
又ON=OM=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
∴MN=
| ||
| 3 |
即
| ||
| 3 |
∴AB=50
| 3 |
∴底边AB的长为 50
| 3 |
故答案为:50
| 3 |
点评:本题是一道立体几何的综合题,着重考查了组合几何体、本题是一道立体几何的综合题,着重考查了组合几何体的面积、体积问题直线与平面垂直的判定等知识点,属于中档题.等知识点,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
 A.
A.

