题目内容
甲、乙两同学进行投篮比赛,每一简每人各投两次球,规定进球数多者该局获胜,进球数相同则为平局.已知甲每次投进的概率为 乙每次投进的概率为1/2,甲、乙之间的投篮相互独立.
乙每次投进的概率为1/2,甲、乙之间的投篮相互独立.
(1)求甲、乙两同学进行一扃比赛的结果不是平局的概率;
(2)设3局比赛中,甲每局进两球获胜的局数为ξ.求ξ的分布列及数学期望.
解:(1)设“一局比赛出现平局”为事件A,
则P(A)= •
• +C21•
+C21• •
• •C21•
•C21• +
+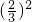 •
• =
=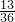 ,
,
所以P( )=1-P(A)=
)=1-P(A)= ,即一局比赛的结果不是平局的概率为
,即一局比赛的结果不是平局的概率为 .
.
(2)设“在一局比赛中甲进两球获胜”为事件B.
因为ξ可取0,1,2,3,
所以P(ξ=0)= =
= ,P(ξ=1)=C31•
,P(ξ=1)=C31• •
•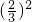 =
= ,
,
P(ξ=2)=C32• •
• =
= ,P(ξ=3)=
,P(ξ=3)= =
= .
.
分布列为:
Eξ=0× +1×
+1× +2×
+2× +3×
+3× =1.
=1.
分析:(1)设“一局比赛出现平局”为事件A,则P(A)= •
• +C21•
+C21• •
• •C21•
•C21• +
+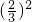 •
• =
=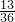 ,再由对立事件的概率能求出一局比赛的结果不是平局的概率.
,再由对立事件的概率能求出一局比赛的结果不是平局的概率.
(2)设“在一局比赛中甲进两球获胜”为事件B.因为ξ可取0,1,2,3,所以P(ξ=0)= ,P(ξ=1)=
,P(ξ=1)= ,P(ξ=2)=
,P(ξ=2)= ,P(ξ=3)=
,P(ξ=3)= .由此能求出ξ的分布列和期望.
.由此能求出ξ的分布列和期望.
点评:本题考查离散型随机变量的分布列和期望,解(1)题时要注意对立事件的概率的运用,解(2)题时要注意n次独立试验恰好发生k次的概率公式的灵活运用.
则P(A)=
 •
• +C21•
+C21• •
• •C21•
•C21• +
+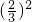 •
• =
=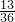 ,
,所以P(
 )=1-P(A)=
)=1-P(A)= ,即一局比赛的结果不是平局的概率为
,即一局比赛的结果不是平局的概率为 .
.(2)设“在一局比赛中甲进两球获胜”为事件B.
因为ξ可取0,1,2,3,
所以P(ξ=0)=
 =
= ,P(ξ=1)=C31•
,P(ξ=1)=C31• •
•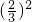 =
= ,
,P(ξ=2)=C32•
 •
• =
= ,P(ξ=3)=
,P(ξ=3)= =
= .
.分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P |  |  |  |  |
 +1×
+1× +2×
+2× +3×
+3× =1.
=1.分析:(1)设“一局比赛出现平局”为事件A,则P(A)=
 •
• +C21•
+C21• •
• •C21•
•C21• +
+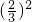 •
• =
=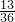 ,再由对立事件的概率能求出一局比赛的结果不是平局的概率.
,再由对立事件的概率能求出一局比赛的结果不是平局的概率.(2)设“在一局比赛中甲进两球获胜”为事件B.因为ξ可取0,1,2,3,所以P(ξ=0)=
 ,P(ξ=1)=
,P(ξ=1)= ,P(ξ=2)=
,P(ξ=2)= ,P(ξ=3)=
,P(ξ=3)= .由此能求出ξ的分布列和期望.
.由此能求出ξ的分布列和期望.点评:本题考查离散型随机变量的分布列和期望,解(1)题时要注意对立事件的概率的运用,解(2)题时要注意n次独立试验恰好发生k次的概率公式的灵活运用.

练习册系列答案
相关题目
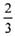 ,乙每次投进的概率为
,乙每次投进的概率为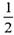 ,甲、乙之间的投篮相互独立.
,甲、乙之间的投篮相互独立. ,乙每次投进的概率为
,乙每次投进的概率为 ,甲、乙之间的投篮相互独立.
,甲、乙之间的投篮相互独立.