题目内容
若x1,x2(x1≠x2)是函数f(x)=ax3+bx-a2x(a>0)的两个极值点。
(1 )若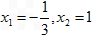 ,求函数f(x)的解析式;
,求函数f(x)的解析式;
(2 )若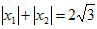 ,求b的最大值。
,求b的最大值。
(1 )若
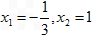 ,求函数f(x)的解析式;
,求函数f(x)的解析式; (2 )若
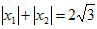 ,求b的最大值。
,求b的最大值。解:(1 )∵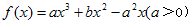 ,
,
∴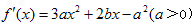
依题意有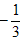 和1是方程
和1是方程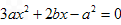 的两根
的两根
∴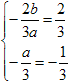
解得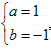
∴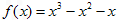 (经检验,适合)
(经检验,适合)
(2)∵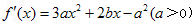 ,
,
依题意,x1,x2是方程f′(x)=0的两个根,
∵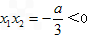 且
且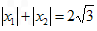 ,
,
∴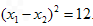
∴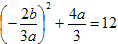
∴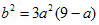
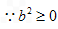
∴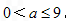
设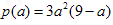 ,则
,则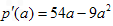
由P′(a)>0得0 <a<6,由P′(a)<0得a>6
<a<6,由P′(a)<0得a>6
即函数P(a)在区间(0,6]上是增函数,在区间[6,9]上是减函数,
∴当a=6时,P(a)有极大值为324,
∴P(a)在(0,9]上的最大值是324,
∴b的最大值为18。
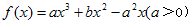 ,
,∴
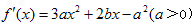
依题意有
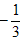 和1是方程
和1是方程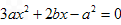 的两根
的两根 ∴
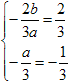
解得
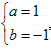
∴
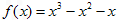 (经检验,适合)
(经检验,适合) (2)∵
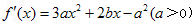 ,
, 依题意,x1,x2是方程f′(x)=0的两个根,
∵
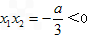 且
且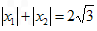 ,
, ∴
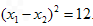
∴
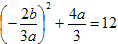
∴
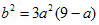
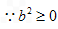
∴
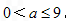
设
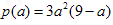 ,则
,则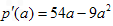
由P′(a)>0得0
 <a<6,由P′(a)<0得a>6
<a<6,由P′(a)<0得a>6 即函数P(a)在区间(0,6]上是增函数,在区间[6,9]上是减函数,
∴当a=6时,P(a)有极大值为324,
∴P(a)在(0,9]上的最大值是324,
∴b的最大值为18。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目